傳說在18世紀(jì)，普魯士國王決定舉行一次盛大的閱兵典禮，計劃從6支部隊中，每個部隊選出6名不同等級的軍官各1名，合計36人，組成一個“6×6”的方陣，要求每行每列都必須有各個部隊和各種軍銜的代表，既不準(zhǔn)重復(fù)，也不能遺漏。這件事情看來很好辦，不料命令傳達(dá)下去之后，卻根本無法執(zhí)行。閱兵司令接二連三地吹哨子，喊口令，排來排去，始終不符合國王的要求。事后，國王對這件事情始終耿耿于懷，然后他就親自編排，可是無論如何編排，都達(dá)不到他當(dāng)初的要求。于是他就去請教當(dāng)時歐洲一流的大數(shù)學(xué)家歐拉，希望能找出一個解決方案。

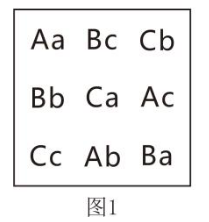
歐拉先從最簡單問題入手，當(dāng)n=3 (即有3種部隊、3種級別)的方陣，用A、B、C表示不同部隊，用a、b、c表示不同級別的軍官，如圖1。這個方陣的特點是每行每列中A、B、C各有一個，a、b、c也各有一個，并且不出現(xiàn)重復(fù)。

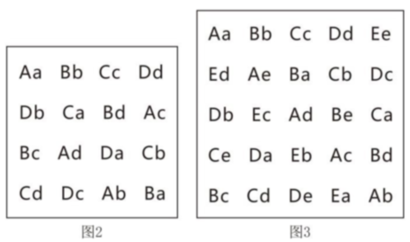
類似的他又寫出n=4、n=5的方陣，如圖2、圖3。它們均滿足條件且又都不重復(fù)。

當(dāng)n=6的情形，既找不到合乎要求的方陣，又不能證明它不存在，但他估計是不存在的。1782年歐拉是這樣談?wù)撨@個問題的:“我已經(jīng)試驗研究了很多次，我確信不可能作出兩個六階的，并且對于10、14，…以及奇數(shù)2倍的階數(shù)都是不可能的。”

歐拉認(rèn)為:4n + 2階歐拉方陣不存在。被后人稱之為“歐拉方陣猜想”。

歐拉“36軍官問題”是組合學(xué)中組合設(shè)計的先聲。由于構(gòu)造正交拉丁方的困難，歐拉方陣猜想的研究進展很慢。直到1910年，加斯頓?塔里在他的兄弟赫伯特?塔里的幫助下，列出了全部六階拉丁方，驗證了它們當(dāng)中任兩個都是不正交的，從而證實了n=6時歐拉猜想是正確的。但人們認(rèn)為塔里兄弟沒有從理論上加以證明，這是一個很大的缺陷，而且隨著階數(shù)增大，列出全部拉丁方的方法也不可取，即使列出全部拉丁方，要驗證每兩個是否正交就更加困難。

1959年4月，印度數(shù)學(xué)家玻色和斯里克漢德構(gòu)造了兩個22階正交拉丁方，從而構(gòu)造出22階歐拉方陣，否定了歐拉猜想。不久，他們證明出:除n=2、6、14、26外，n階歐拉方陣都是存在的。接著，美國數(shù)學(xué)家帕克又構(gòu)造出14階與26階的歐拉方陣，至此，歐拉方陣猜想只對當(dāng)n=2、6成立，其余都是錯的。這個否定的結(jié)果是人們在180年的努力中未曾想到的。

類似這樣的方陣，在工農(nóng)業(yè)生產(chǎn)和科學(xué)實驗領(lǐng)域都有極其廣泛的應(yīng)用，利用它能夠以較少的實驗次數(shù)獲得較好的結(jié)果，還能節(jié)省原料，改進配方等等。

本作品為“科普中國-科學(xué)原理一點通”原創(chuàng)，轉(zhuǎn)載時務(wù)請注明出處。

?

三十六軍官問題

圖文簡介

傳說在18世紀(jì)，普魯士國王決定舉行一次盛大的閱兵典禮，計劃從6支部隊中，每個部隊選出6名不同等級的軍官各1名，合計36人，組成一個“6×6”的方陣，要求每行每列都必須有各個部隊和各種軍銜的代表，既不準(zhǔn)重復(fù)，也不能遺漏。