作者:易疏序
編輯:婉珺
你可能經常看到這樣的說法:引力可以讓時空彎曲。不過你會發現無論這句話看著多么眼熟,還是理解無力。
其實這沒有什么可自責的。我們可以理解一張紙是彎曲的,是因為我們站在紙外。換句話說,我們站在更高維的空間(3維)觀察一個低維空間(2維)的幾何性質(彎曲)是很容易的。但去理解時空的彎曲就是非常反直覺的了,因為“不識廬山真面目,只緣身在此山中”,我們身處這個時空,又如何知道時空是彎曲的呢?
為此,我們今天祭出一件上古神器— 指南車 ,它可以幫助你理解 “我們怎么知道時空是彎曲的”。
傳說5000多年前,黃帝與炎帝的聯軍同蚩尤部落決戰于涿鹿之野。蚩尤作法,用濃霧困住黃帝的軍隊。黃帝發明了指南車,并借此辨認方向沖出濃霧并戰勝了蚩尤。據描述,指南車上有一木制小人像,一只手臂抬起指向前方。無論車身如何運動轉向,小人的手臂始終指向同一方向。
黃帝的傳說過于久遠而不可考證,不過指南車確實散見于從周到宋間兩千余年的史書中。其中《宋史》里很詳細地描述了指南車的結構和原理。現代人根據宋史中的描述,成功地復原出了指南車。

復原出來的指南車。圖片來源:Wikipedia
指南車的原理并不復雜。它有兩個輪子,當車子轉向時,兩個輪子的轉速會產生差異。這個轉速的差別會通過差動齒輪裝置驅動小人轉向。經過矯正和調試,小人轉向的角度恰好可以補償車子的轉向,于是 無論車子如何轉向,小人都指向同一個方向。
如果指南車不是行進在平地(平面)上,而是行進在崎嶇的山地(曲面)上還能否奏效呢?
我們考慮一種最簡單的情形。
指南車一個輪子固定,轉動另一個輪子使車原地轉一圈。在平地上的時候,那個轉動的輪子走過的長度是兩倍的軸距乘以圓周率,通過差速器,小人向反方向旋轉360°,正好補償了車子的轉動,因此小人抬起的手臂指向原來的方向。而如果車停在一個小山包上,那么轉動輪子所畫出的圓周的周長就會比這個數字小。
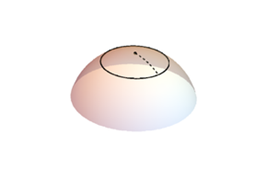
所以,差速器傳遞給小人的轉向角就會小于360°,因此小人的手臂就會偏離原來的方向:小車向左轉,小人的手臂就向左偏,反之亦然。同樣的,當小車停在一個小山坳里時,也是類似的情況。
另外有一種比較奇葩的地形,叫做 雙曲面 (也可以叫馬鞍面或者薯片形)。
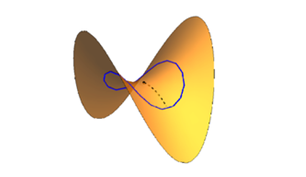
在這種地方圓周會變大。因此指南車行走在這樣的地形上,小人手臂的轉動會超過需要補償的角度:小車向右轉,小人的手臂卻向左偏,反之亦然。
在幾何學中,這兩種不同的情形可以用 高斯曲率 這個概念區分。
原來,不論是山包還是山坳,它們的高斯曲率都是大于零的,而雙曲面的高斯曲率卻是小于零的。
我們可以進一步證明 [1] ,指南車出去兜一圈回到原點,小人手臂是否偏離原來的方向,這取決于指南車巡游路線所包圍的曲面中所有點上的高斯曲率的總和。
這里面提到的高斯曲率是一個曲面的 內稟性質 ,也就是 不會隨外界環境變化而改變的性質 。什么意思呢?比如一張紙,它展平的時候高斯曲率處處都等于零,那么無論你如何彎曲這張紙,只要不撕裂,它的高斯曲率始終是處處為零。同樣,球面的高斯曲率是大于零的,因此球面無論如何也無法被拍扁成一個平面。
所以說, 有了指南車這個神器,人們可以不必跳出大地便能測量大地的幾何性質。 順便說一下,幾何(Geometry)這個詞是希臘語詞根Geo-意思是大地,metry意思是就是測量。
空間有三個維度(上-下,左-右,前-后),時間有一個維度(過去-未來),合起來是一個3+1維的時空。我們居住在其中,無論如何也跳不到一個更高維的空間去測量時空的形狀。因此,我們大多數人都很難理解,什么叫“彎曲的時空”。即便如此,我們可以利用類似指南車的原理,不必跳出這個時空也能知道時空有沒有“彎曲“。
陀螺儀就是時空里的“指南車”。 在平直的時空里,不受力矩的陀螺儀的轉軸總能保持指向一個方向。可是如果一個陀螺儀出去兜了一圈回來發現它的轉軸居然偏離了原來的方向,這時候你就知道陀螺儀所處的時空有內稟的曲率,也就是說時空是彎曲的。

陀螺儀。圖片來源:shutterstock
按照廣義相對論, 有質量的物體就會使它周圍的時空彎曲 。因此,一個陀螺儀放在衛星上,繞著地球轉幾圈之后久能看到陀螺儀的轉軸發生明顯的轉向。這就是所謂的“ 測地線進動 (Geodetic Precession)”,這種效應已經被NASA 2004年發射的衛星Gravity Probe B 所證實 [2] 。

2004年發射的衛星Gravity Probe B。圖片來源:wikipedia
也許在“高維生物”的眼中,我們是匍匐在“地面上的渺小螞蟻”,永遠也無法離開“地面”看一眼“大地”。但我們雖然渺小,卻不卑微。因為我們擁有智慧,能造出“指南車”,它讓我們不必跳出“地面”便可以知道“大地”形狀。

作者名片

排版:小爽
題圖來源:cbsnews
參考文獻:
[1] 已經有研究證明,指南車小人手臂相對于車身的轉動角度等于小車路徑上的測地曲率的積分,而測地曲率的積分又可以用Gauss-Bonnet定律和高斯曲率的面積分聯系起來。參考:鄧崇林 蕭先雄 指南車在物理學中幾何相位的應用- 《物理與工程》2014年 第S2期
[2]http://einstein.stanford.edu/content/final_report/GPB_Final_NASA_Report-020509-web.pdf



 科普中國公眾號
科普中國公眾號
 科普中國微博
科普中國微博

 幫助
幫助