亚洲 激情 小说 另类 欧美,无码在线播放一区,99 久久 国产 欧美,污视频网站在线观看二区

　　量子力學求解的困難 

　　上世紀初出現的量子力學為我們研究微觀世界的運行機理提供了強有力的工具，似乎所有的問題都可以通過求解一個薛定諤方程來解決。但在實際應用過程中卻發現能夠精確求解的體系實在是少之又少，即便是最簡單的氫原子求解起來也并不容易，對于更加復雜的凝聚態體系更是無從下手。 

薛定諤方程（圖片來源：百度百科） 

　　因此，尋找可以描述凝聚態體系性質的簡單模型和行之有效的近似方法稱為物理學家的研究重點之一。贗勢方法和經驗贗勢方法就是其中強有力的代表，于1998年獲得諾貝爾化學獎的密度泛函理論也和這兩種方法密切聯系。 

Walter Kohn，密度泛函理論創始人之一（圖片來源：百度百科） 

　　我們知道，無論在經典力學力還是在量子力學里，單粒子問題都是最好解決的。所以我們自然會想到，是否可以通過對單粒子體系的計算來理解多粒子體系的行為？不過，即使對于單粒子體系的求解也會因為勢場在空間中的波動使計算變得困難（尤其是在計算機還沒有出現的時候）。幸運的是，（經驗）贗勢方法可以較好地解決這兩個問題。 

　　贗勢方法 

　　贗勢的概念最早是費米在研究高激發態電子時引入的。之后，赫爾曼嘗試用贗勢方法計算堿金屬的能級。到1950年左右，贗勢方法開始廣泛應用到凝聚態物理領域。贗勢方法之所以好用是因為很多時候我們只需要考慮價電子的行為，而芯電子可以和原子核一起組成一個整體，這樣價電子就像在一個微弱的單電子勢中運動。這讓整個計算變得簡單很多。 

恩里克 · 費米（圖片來源：科學網） 

　　基于正交平面波（OPW）方法的贗勢最早由Herring引入。在正交平面波方法中晶體波函數和芯電子波函數正交并用布洛赫函數和芯電子態進行展開。我們可以引入離子吸引勢計算芯電子態，再利用的引入排斥勢計算布洛赫函數。吸引勢和排斥勢的共同作用使得總勢場在空間中變化緩慢，相應地，場強很弱。這套方法被稱為Phillips-Kleinma方法，它也證明了為什么金屬中價電子的行為表現得像近自由電子。 

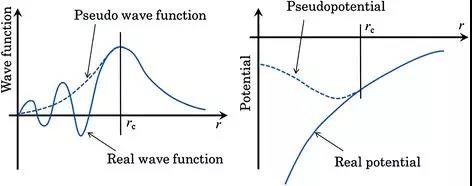
贗勢和真實勢場對比（圖片來源：維基百科） 

　　之所以在贗勢中引入吸引部分和排斥部分是因為在接近原子的區域，勢場主要由原子實提供，表現出強烈的吸引作用，在其他區域由于電子屏蔽等作用，吸引勢被抵消，這也是我們引入排斥勢來抵抗吸引勢的原因。 

　　經驗贗勢法 

　　前面提到的Phillips-Kleinma方法將計算能帶的問題簡化成一個單電子問題。但想要直接確定贗勢仍不是一件簡單的事情。在前人工作的基礎上，Cohen等人發展出經驗贗勢方法。 

　　這種方法將贗勢計算和晶體自身的獨特對稱性聯系起來，贗勢的形式會受到對稱性的很多的限制，因此可以大大減小我們計算贗勢時的難度。 

　　由于晶體具有平移對稱性，我們可以假定電子感受到的單電子勢場也具有周期性。一般地，通過傅里葉變換可以將晶體勢場按照倒格矢進行展開。這看起來好像并沒有讓問題變簡單，但是對于實際應用來說，當階數很大時，分量的系數會變得很小以至于可以忽略不計。如果再考慮到對稱性的限制，我們往往只需計算少數幾個系數。 

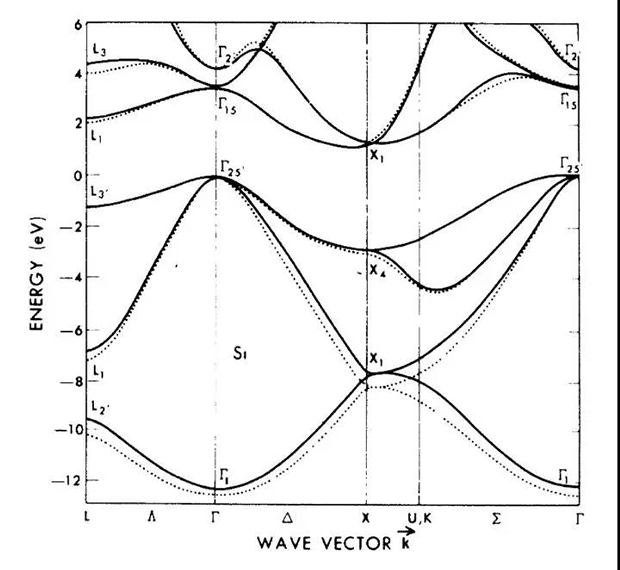
局域贗勢（虛線）和非局域贗勢（實線）計算得到的能帶（圖片來源：physics.upenn.edu） 

　　在實際的使用中，我們需要幾個初始的系數，通過一系列手續計算出能帶和可以直接測量光電等性質，然后和實驗得到的數據進行比較，如果和實驗符合則計算結束，如果和實驗不符則修改系數重新計算直到可以吻合。 

　　影響 

　　（經驗）贗勢方法的出現使得對凝聚態體系的理論計算稱為可能，它從科學上闡明了很多我們之前不理解的問題，如為什么雖然金屬中既有電子又有離子實但是電子的行為和自由電子非常像。 

　　在應用中，經驗贗勢方法為半導體工業起到了強大的指導作用。半導體工業的發展催生了計算機技術的進步。有趣的是，計算機技術的進步反過來促進了（經驗）贗勢方法的發展。 

　　參考文獻: 

　　[1]  E. Fermi, Nuovo Cimento 11, 157 (1934). 

　　[2]  H.J. Hellman, J. Chem. Phys. 3, 61 (1935). 

　　[3]  J. C. Phillips and L. Kleinman, Phys. Rev. 116, 287 (1959). 

　　[4]  J. R. Chelikowsky and M. L. Cohen, Phys Rev. B 10, 12 (1974). 

　　[5]  J. R. Chelikowsky and M. L. Cohen, Phys. Rev. B 10, 5059 (1974).