熵與信息(二):熱力學熵和信息熵,是同一個熵嗎?
信息是什么?在上一集我們就提到過,信息可以降低一個系統的不確定程度。這句話里其實就已經暗含了對熵的描述。熵是對一個系統不確定的度量,而信息可以降低不確定性。
也就是說,熵和信息一定是有關系的,只要我們找到其中的關系,就能把熵是什么搞清楚了。
這件事香農做到了。而且香農定義的熵是基于信息量得出來的,所以也叫做信息熵。
那么信息熵是什么呢?就是簡單的把一個系統可以發出的所有信息的信息量加起來嗎?沒有那么簡單。
信息熵
還是用第一集里簡化版的“世界杯比賽”來舉例,從 8 個球隊比賽不知道誰得冠軍,到確定阿根廷奪冠。賽前這個系統是不確定的,當決賽完成之后,冠軍就成了確定的了。

這個過程從定性的角度去理解很容易,可是如何定量的去衡量 8 支球隊比賽之前的這個狀態到底有多不確定呢?
在比賽之前最大的特點就是,我們并不知道誰會真的奪冠,而不同的球隊奪冠,所帶來的信息量也是不同的。
比如說,我們只看阿根廷隊和中國隊,阿根廷是強隊假如他們奪冠的概率 50%,中國隊是弱隊奪冠的概率是 1%。有兩個消息,一個是阿根廷奪冠了,一個是中國隊奪冠了,那么根據上一集計算信息量的公式:
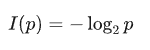
可以計算出來,阿根廷奪冠這個消息的信息量是 1 bit,而中國隊奪冠的信息量則大概是 6.6439 bit。
一共 8 支球隊,每支球隊都可以根據自己賽前的奪冠概率計算出,假如自己奪冠了,這條消息所具有的信息量。
所以,一個非常直接的想法是,如果要確認賽前“世界杯比賽”這個系統的不確定性,是不是可以把各自球隊奪冠后的信息量加起來表示呢?這個直接相加后的信息量,會不會就是這個系統的熵呢?
不能這么做,這樣做之后會讓熵這個概念出現矛盾。比如,我們可以簡化一下問題,分別看兩場比賽,一場是阿根廷和法國隊比賽,他們各自贏球的概率都是 1/2,另一場比賽是德國隊和中國隊比賽,德國隊贏球的概率是 99%,中國隊只有 1%。
可以分別計算一下他們贏球之后所具有的信息量。
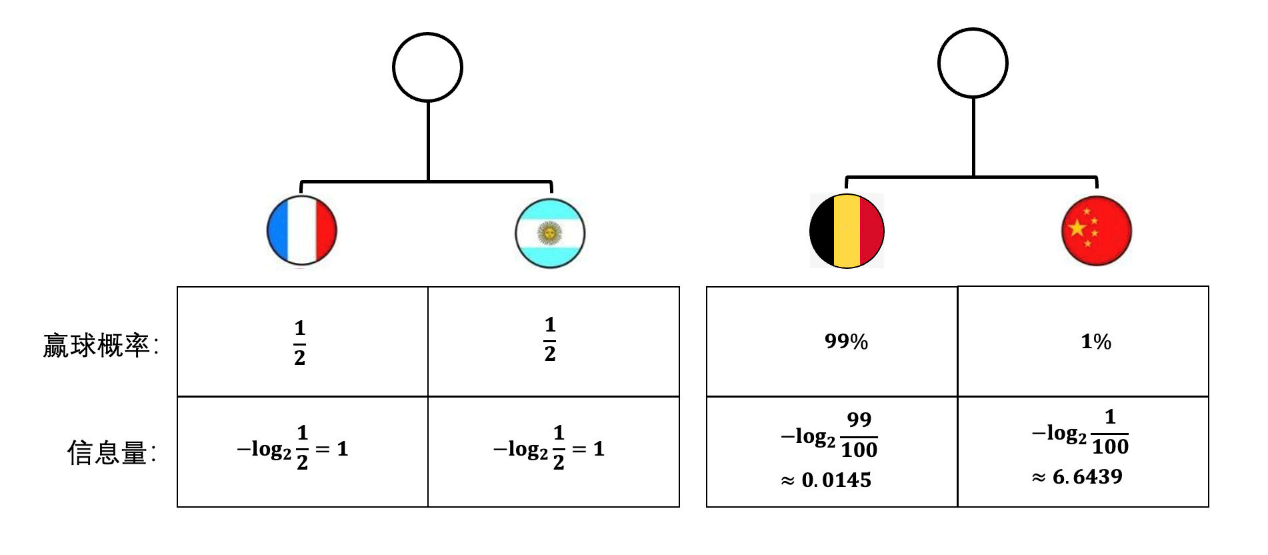
如果系統的熵就是簡單的把信息量加起來的話,那么可以看到阿根廷和法國在賽前的熵應該是 2 ,而德國和中國呢,則是 6.6 還要多。還記得我們對熵是如何期待的嗎?期待它是對系統不確定性的度量,一個系統不確定性越高,熵應該越大。
但是我們可以從直覺上判斷一下,是阿根廷和法國這場比賽的不確定性更高呢,還是德國和中國的比賽不確定性更高呢?肯定是第一場對吧,德國 99% 的概率是會贏球的,這個確定性非常非常高了。這個就和我們前面計算出來的熵的數值不匹配了,前面計算出來反而是第一場是 2bit,第二場至少有 6.6bit。
這顯然不合理對吧。為什么呢?
別忘了,中國隊要想真的能夠貢獻那么多的信息量必須有一個前提,那就是中國隊需要真的奪冠才行。中國隊奪冠的概率是多少?只有 1%。所以,如果這個角度再去考慮不同結局對整個系統貢獻了多少信息量的話,應該是先要進行一個加權處理的,讓信息量乘以它發生的概率。
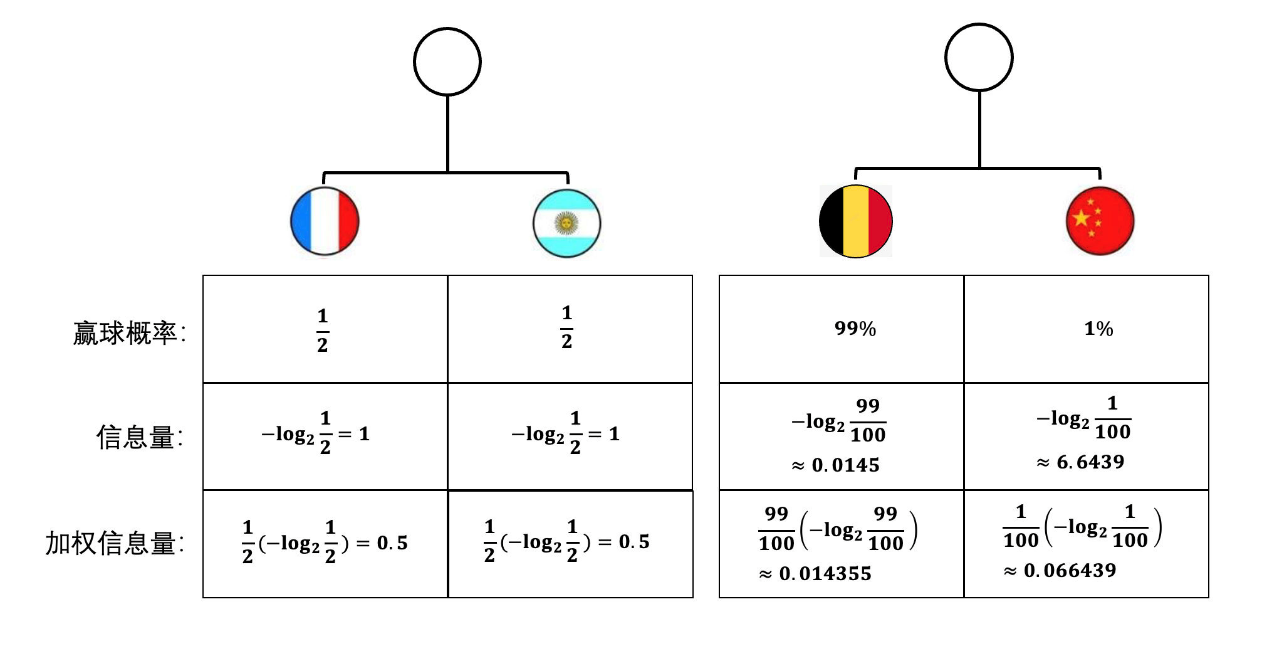
這個時候再看把它們加起來,那第一場比賽的熵是 1bit,第二場比賽的熵只有 0.08bit 左右,第二場比賽的熵遠小于第一場。這樣就比較合理了。如果用數學符號表示出來,就是這樣:
假如系統 X 一共有 n 種可能,那么:
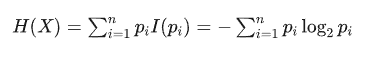
如果對概率論有些基礎的話,就會發現,熵其實就是一個系統里信息量的平均值(期望值):
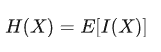
這也是香農對熵的定義,從信息量的角度定義出來的熵也被稱為信息熵。
信息熵并不是對熵這個概念的唯一定量描述。除了信息熵,還有熱力學熵,熱力學熵里面也還有克勞修斯熵、玻爾茲曼熵、吉布斯熵等等不同等表述。
這并不是說它們是不同的東西,而是從不同角度分別對“熵”的概念進行的不同描述。它們雖然本質上是等價的,但是都有各自的應用領域,對于我們的理解也各有優勢和劣勢。
比如,信息熵雖然簡單直觀,但是它卻很容易讓人產生一個困惑,那就是熵似乎是一個非常主觀的量化指標。
比如在開賽之前,不同人對 8 支球隊奪冠概率的概率是可以非常不一樣的。這就代表著,不同人面對同一個世界杯比賽,會得出不一樣的熵。
熵是主觀的?
只要是基于信息量去理解熵,那么這個熵的主觀性問題就天然存在。
因為一提到信息,必然涉及到一個通訊過程中,也就是一定有兩個系統,一個是信息發送者,一個是信息接收者。在前面的例子中,世界杯比賽是信息發送者,這個是客觀的,但是不同人對不同的球隊可以有不同的估計。
這樣,同樣的一個信息,對于不同的接收者就會帶來不同的信息量,反推回去,在不同的人眼中,同一個信息發送者的熵就會有不一樣的數值。
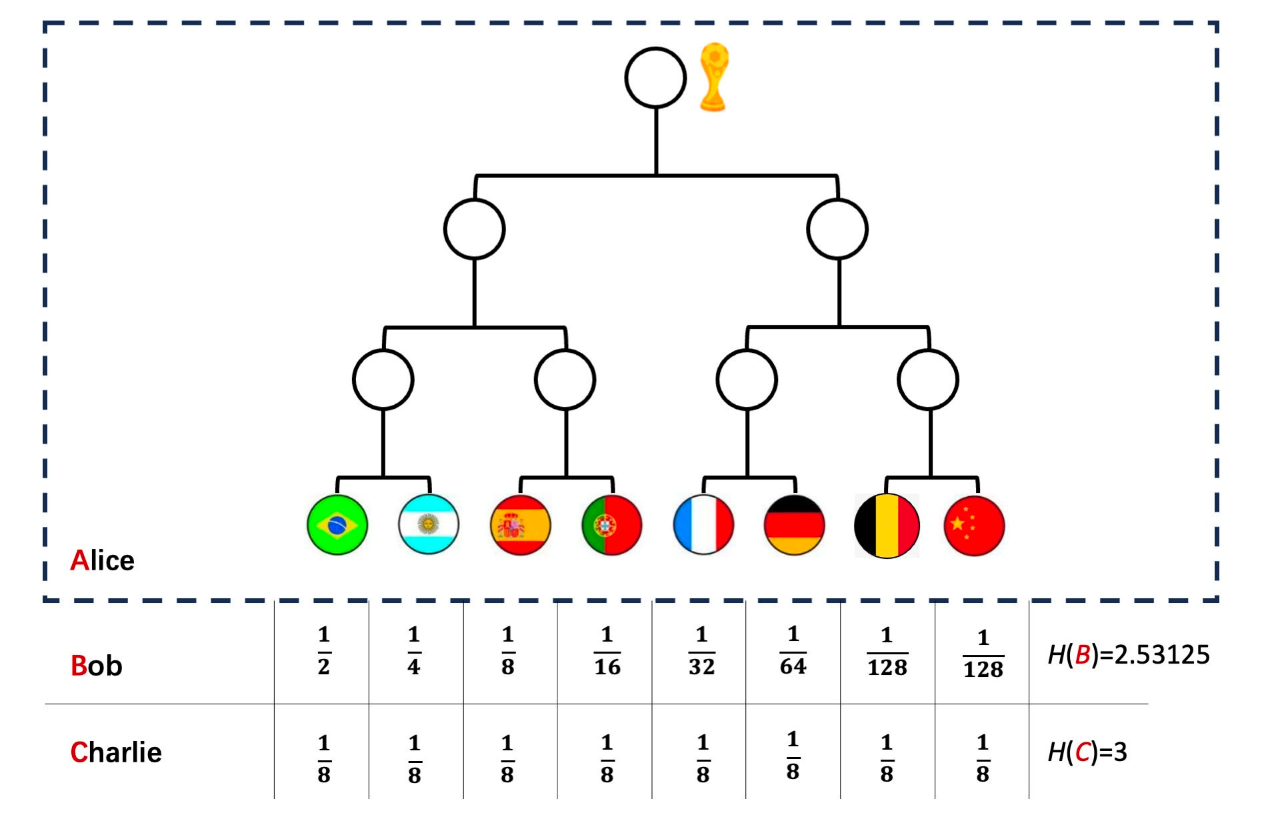
這里的“主觀性”其實就體現在通訊過程必須同時存在兩個系統,我們把發送者稱為 Alice,接受者稱為 Bob。發送者 Alice 的狀態是一定的,熵只和系統的狀態有關,所以他的熵應該也是一定的,也就是說它有一個客觀的數值的。
但是發送者(Alice)和接受者(Bob)之間傳遞的信息并不直接取決于發送者(Alice)的熵,而是取決于發送者(Alice)和接受者(Bob)兩個系統里熵的交集(雖然這么表示不嚴謹,但仍然可以先這樣理解)。
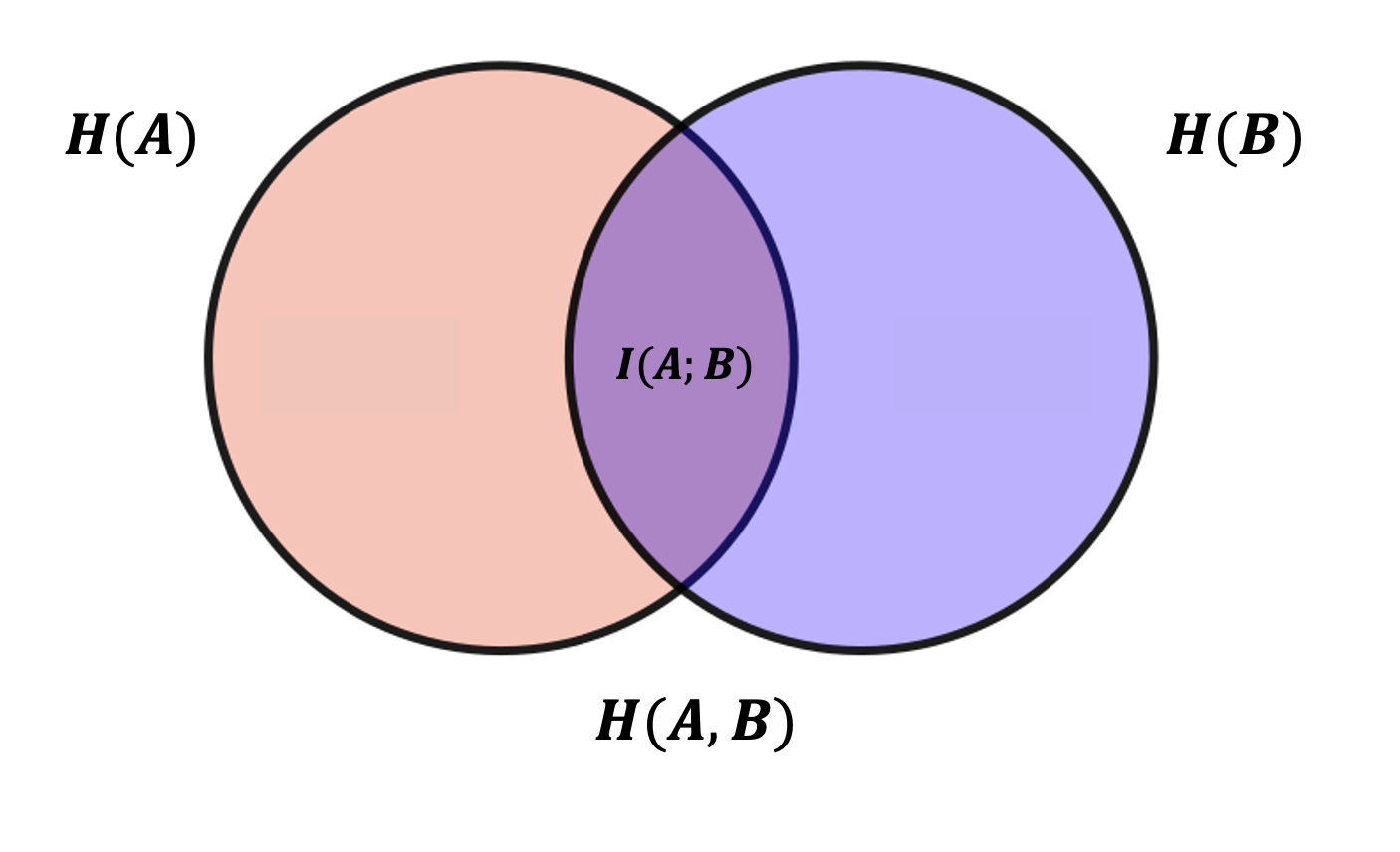
不同的接受者計算出來不一樣的“信息熵”,其實是發送者和接收者交集那部分的熵,嚴格意義上來說這部分應該叫做互信息,用來 表示。
只有在接受者的熵完全包含了發送者(Alice),這個時候的互信息才完全等于發送者的熵。如果有 Bob 和 Charlie 兩個接受者,它們可以不一樣,但是都完全包含了發送者的熵,那么不論 Bob 和 Charlie 多么不一樣,他們按照我們前面的做法計算出來的“信息熵”就一定是由發送者 Alice 自身客觀決定的。
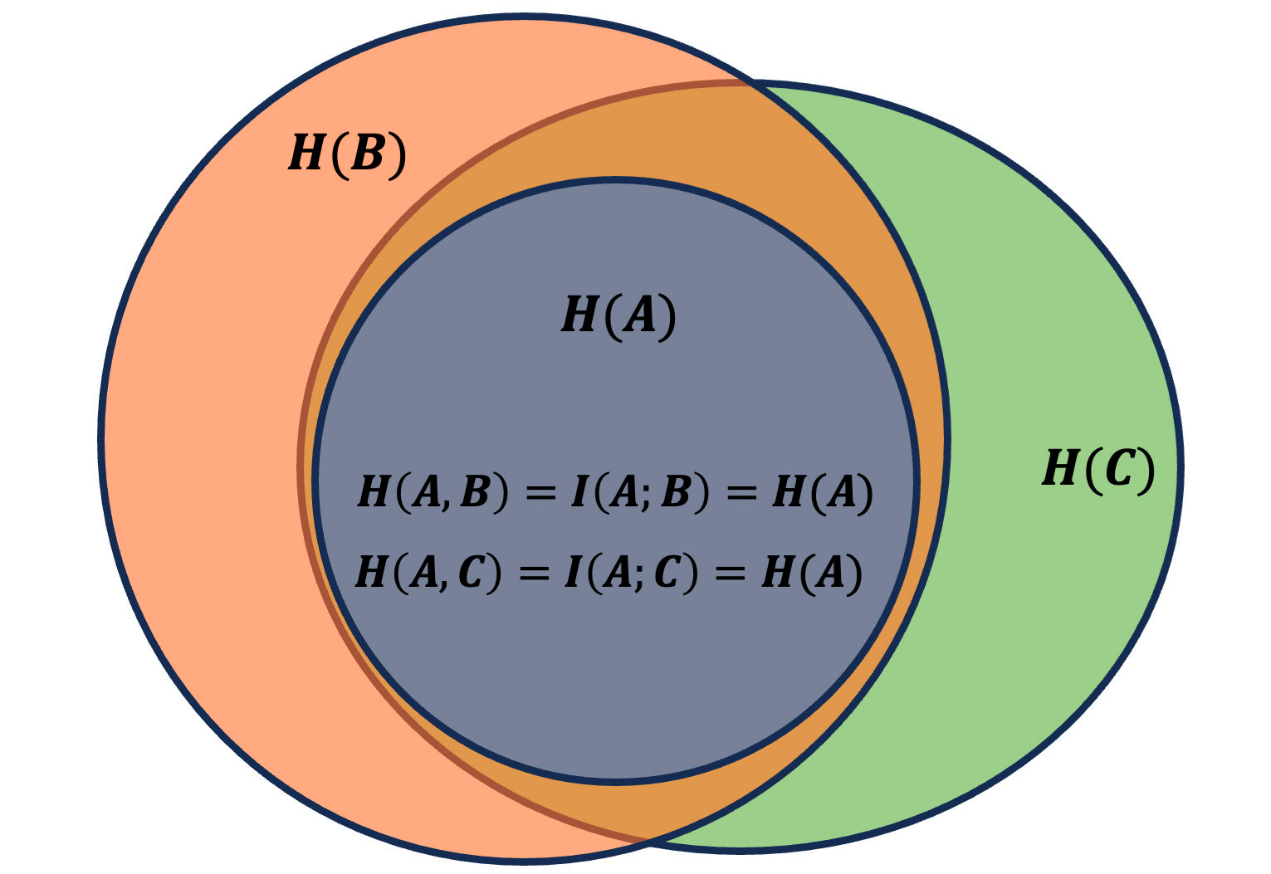
要想徹底理解互信息這個概念,需要鋪墊一些通訊的知識。這次篇幅不夠了,后面會專門介紹一下熵和信息量在通訊領域的作用,到時候再理解這件事就容易了。
不過,即便是通過前面的簡單介紹,大家應該有這樣一個想法了,信息熵的主觀性主要還是因為需要同時考慮發送者和接受者兩個系統。那么,如果只單獨考慮一個系統的熵,是不是就可以完全將“熵”的主觀性排除了呢?
也沒有那么簡單,我們可以來看一下這樣一個例子。
從科普的角度去解釋熵,一個經常用的方式就是拿一副撲克牌來舉例。一副新撲克牌,它里面牌的大小和花色都是整理好的,所以這個時候的牌熵就小。

如果開始洗牌,撲克牌的順序就會被打亂,這個時候就代表著熵增。而且在最開始幾次洗牌的過程中,撲克牌的次序會越來越亂,也就是熵越來越大。直到撲克牌的次序達到一個幾乎隨機的狀態,此時熵達到了最大,即便繼續洗牌熵也不會增加了。
很多人看到這個例子之后,都會產生這樣的疑問,這里對于撲克牌“有序”的標準是如何定義?必須按照從 A 開始、2、3、4…… 這樣排列下去嗎?為什么不能隨便規定好一個順序,認為這是最有序的?
如果隨便規定一個次序標準,那么一幅新牌相對于標準反而更加混亂。這樣的話,豈不是一個系統的熵要依賴于對于“有序”是如何定義的了嗎?這應該也是一種“主觀”吧?
這其實有點像是勢能,對 0 勢能的位置定義不一樣,一個系統的勢能的具體數字是不一樣的。雖然勢能的絕對值是不一定的,但是從一個狀態到另一個狀態,勢能增加和減少的大小卻是一定的。而且勢能最后的大小,只和開始和最終的狀態有關,和中間的變化無關。從高處 A 落到 B 點,不論是直接下落,還是先拋起來再下落,最后勢能的改變值都是一樣的。
熵也是類似的情況,在一個狀態正在變化中的系統中,熵改變的多少只和初始、最終的狀態有關,和具體的變化過程無關。所以,現在看來似乎只有熵變化量才是絕對的,熵的絕對值肯定是主觀的。
這樣理解沒有問題,但是也有例外。以撲克牌為例,從一副新撲克牌開始洗牌,剛開始的時候每洗一次,撲克牌就會被打亂一次,隨著洗牌的次數增加,撲克牌的混亂度越來越高,這也代表著撲克牌的熵在逐漸增加。

但需要注意的是,撲克牌混亂程度并不會一直增加下去,洗牌到一定次數之后,撲克牌已經足夠混亂了,再多洗幾次牌也不會讓撲克牌更加混亂。這個時候也就代表著熵不再增加了。這其實就說明這個撲克牌在這種洗牌手法下已經達到了平衡狀態了。
平衡狀態下的撲克牌的熵就是確定的了,這當然也就是客觀的了。也就是說,不論你設定的標準“次序”,只要洗牌的次數夠多,那么就會達到一個確定的熵值,而且這個熵值還不依賴于任何主觀因素。
如果把撲克牌換成氣體,一張一張的牌就是氣體里的分子,牌的順序就是氣體分子的各種狀態,洗牌就是氣體分子的隨機熱運動。那么一幅牌從全新狀態洗牌到完全混亂的過程,完全可以看作是把各種不同的氣體混合到一起之后,隨著熱運動的作用,氣體分子變得充分混合,達到了平衡狀態。
這個平衡狀態的熵就是客觀且確定的。而這里用來描述氣體的熵其實就屬于熱力學熵了,而熱力學熵中最有名的就是玻爾茲曼熵。
熱力學熵
玻爾茲曼熵的定義是這樣的:
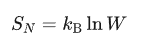
這里的 S 就是玻爾茲曼熵, 是玻爾茲曼常數,國際標準下
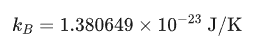
作為熵的定義,對數計算肯定是少不了的,不過對數計算 ln 里面的 W 就和信息熵有些不太一樣了。在信息熵定義中,進行對數運算的是概率值,而這個公式里的 W 不是概率值,它某種程度上就可以代表一個系統在熱平衡狀態下的混亂程度。有的地方也用 Ω 表示。
這個混亂程度更準確的說法是“給定宏觀態對應的微觀態的數量”。這里有兩個關鍵詞,宏觀狀態和微觀狀態。如果用理想氣體舉例的話,宏觀狀態就是這個氣體的總能量、體積、壓強、溫度等物理量。微觀狀態就是氣體里的單個分子狀態,往往也就是氣體分子的動量和位置。
或者更直觀一點,可以把分子可以具有的微觀狀態想象成是一個一個的小格子。不同格子代表著氣體分子的不同微觀狀態,每個氣體分子都會根據不同的狀態放到這個格子里面。如果兩個分子的動量不同,那么就放到兩個不同的格子里,如果兩個分子的動量相同那就放到相同的格子里面。
“給定宏觀態對應的微觀態的數量”,這句話有兩層含義。
第一層,確定一個宏觀狀態(比如是標準大氣壓、20攝氏度、一升純氧氣)之后,在平衡狀態下每個微觀狀態的格子里面的分子數都是確定的。
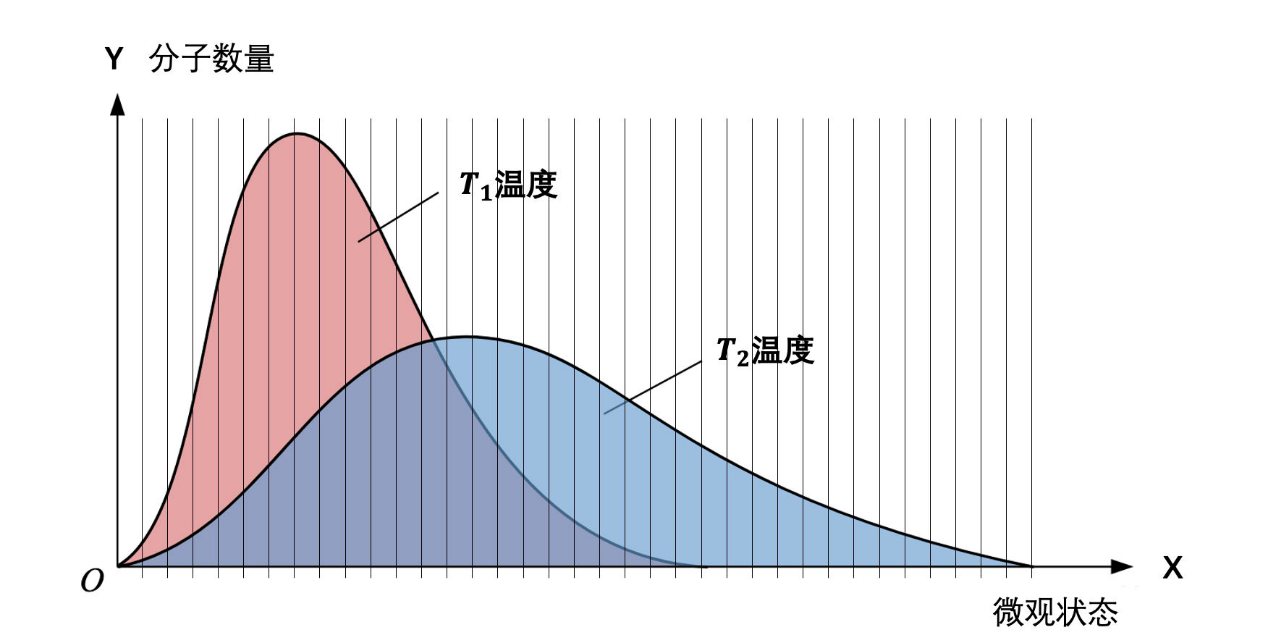
如果我們就是停留在第一層,這個宏觀和微觀的對應關系,也完全可以描述出該系統的混亂程度。就像圖中里描述的,不同溫度分別對應不同的曲線。
玻爾茲曼熵里面的 W 就是代表這個曲線的話,那這個 W 應該是至少應該是一個二維數組才行。
比如像圖中描述的那樣,一共有 N 個分子,需要放到 K 個不同盒子里面。不同的溫度會有不同的分布圖。如果想把 溫度的分布表述出來,那么一定是需要將 1 到 K 個盒子里的分子數全部表示出來,可以寫作:
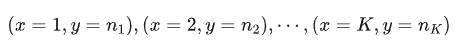
這樣的二維數據顯然沒有辦法直接進行 ln 運算,所以在玻爾茲曼熵的公式里面,這個 W 必須是用一個具體的數值表示才行。
這個時候就需要理解“給定宏觀態對應的微觀態的數量”這句話里的第二層含義了。
這句話里說的“數量”并不是每個微觀狀態盒子里的分子個數,而是要統計一下在氣體處于當前 (比如 )的分布曲線的情況下,一共可以有多少種可能性。
假如說,氣體里面一共有 N 個分子、K 個微觀狀態盒子,那么 W 應該等于把 N 個分子,按照分布曲線裝入 K 個盒子里面一共有多少種可能性。
具體怎么做呢,我們可以一步一步地來。
把 N 個分子裝到第1個盒子里,第1個盒子在一個 溫度下能且只能裝 個分子,相當于從 N 個里面挑 個,所以一共有 種情況。然后看第 2 個盒子一共可以裝 個分子,因為還剩下的 個分子,所以一共有 種情況。以此類推,所有的情況都可以寫出來然后相乘就是最后總的可能性了。具體如下:
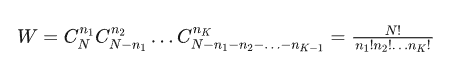
這種總數,比起二維的數據一定是丟失了信息的,但是對于一個系統整體的熵已經足夠了。丟失的信息是什么呢?這部分丟失的信息,代表著無法把某個具體的微觀狀態里會有多少分子還原出來。也就是說理論上存在兩個系統熵相同,但微觀狀態不同的情況。
有了玻爾茲曼熵的基礎,再去看撲克牌洗牌這個熵增的過程,就可以做一些定量的分析了。
為了方便我們簡化一下洗牌的方法,每次洗牌都會讓一張牌隨機出現在它原本次序的正負 2 格之內。原來一張牌的位置是 10,那么洗牌 1 次,它就可能隨機出現在 8 到 12 任意一個位置。如果洗牌 2 次,那么最開始位置 10 的那張牌,就有可能出現在 6 到 14 的任意一個位置上。
當然這個時候 6 到 14 這幾個位置對應的概率還是不一樣的,6 和 14 要小一些 (畢竟要連續減 2,或者連續兩次加 2),9、11 的概率就要大一些,10 的概率值最大。總之就是一個類似正態分布的情況。
隨著洗牌的次數增加,最開始 10 號位置的牌,就可能出現在任意一個位置,而且每個位置出現的概率還會趨于平均。到了這個時候就達到了熵最大的情況,也代表著達到了平衡狀態。
從熱力學熵到信息熵
其實講到這里,玻爾茲曼熵和信息熵互相之間還是割裂的,因為決定玻爾茲曼熵大小的是 W,而 W 是一個和個數有關的數量值。信息熵就完全不同了,信息熵里面起決定性因素的是概率值。一個是數量值,一個是概率值,這互相之間應該如何產生聯系?
其實也很簡單,因為某個事情發生的次數除以所有情況都發生的次數得到的就是概率值。反過來,一個概率值的倒數,其實就可以理解為是這個事件發生的次數。
所以,次數和概率值互相之間是可以互相轉化的。只不過玻爾茲曼熵里的 W 要想轉化成概率值,還需要借助一下斯特林公式:
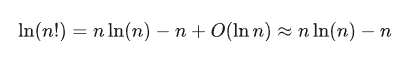
其中 是關于 的一個無窮小量,所以在 n 很大的時候它可以忽略。
具體如何利用斯特林公式將玻爾茲曼熵的形式變成像那樣的信息熵的形式,就需要一些數學推導了。其中涉及的數學知識不會超過高中,感興趣的話可以詳細看一下。如果不看也沒關系,知道次數和概率是可以相互轉化的就可以了。
具體的推導過程如下:

這個其實就已經是吉布斯熵了,可以看出它和信息熵的形式幾乎一致,都是以
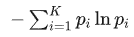
作為主體,不一樣的只是對數運算的底和一個常數系數。雖然前面的推導過程并不那么嚴謹,不過還是可以從中看出熱力學熵和信息熵本質上都是相同的。
而這也是為什么馮·諾伊曼看到香農的公式之后,讓他把它叫做熵的原因。
熵本來是一個熱力學里的概念,但是自從它和信息之間的聯系被發現之后,原來在物理體系下很難得到的解決的問題就可以被更容易解決了。這其中最有名的就是物理學四大神獸之一的“麥克斯韋妖”了。
但是要想解決這個問題,那就需要通過熵將信息和能量的關系建立起來。我們下一集就一起來討論這個問題。
來源: 上海光錐文化傳媒有限公司
內容資源由項目單位提供


 科普中國公眾號
科普中國公眾號
 科普中國微博
科普中國微博

 幫助
幫助
 2024年度科普中國資源薈萃集成示范項目
2024年度科普中國資源薈萃集成示范項目 