“他清楚自己擁有那個時代最睿智的頭腦,這是他自負的資本,但是他的自卑也是明顯的,一旦有很多人站在他的對立面,他就會惴惴不安,反復思考自己是否有這樣或那樣的錯誤……”
——愛因斯坦
撰文 | 鄭超(中國科學院上海有機化學研究所研究員)
前情提要
我們前不久在上篇文章中講述了“物質由不可分割的原子組成”,是起源于古希臘的古老思想。十九世紀初,道爾頓跳出哲學思辨的藩籬,以物質的化學組成問題為依托,提出了近代原子論。一石激起千層浪,以原子為基礎理解化學反應的觀念助力了十九世紀化學的蓬勃發展。1860年,坎尼扎羅在卡爾斯魯厄會議上傳播阿伏伽德羅的分子學說,進一步推動了原子、分子概念在化學研究中的應用。然而,原子和分子從科學概念最終走向物理實在,還有漫長的道路等待著人們去探索和跋涉。
本文繼前文繼續講述……。
唯能論者的阻擊
雖然坎尼扎羅在卡爾斯魯厄會議上澄清了許多關于原子、分子概念的誤區,但是遠未消除化學家們心中的疑慮。凱庫勒在1867年的論述最能體現這種矛盾的心態。他說作為化學家,他“完全認同原子和分子不僅是明智的假設,更是不可或缺的需要”;但是作為哲學觀點,他“并不相信原子和分子是構成物質的基本單元”。畢竟當時的化學分析手段非常有限,遠不足以論證“道爾頓發明的堅硬小球”的存在。在相當一部分化學家看來,原子和分子不過是表征物質元素組成的一種便利模型罷了。“東方不亮西方亮”。有關分子存在性爭論的陣地,在十九世紀下半葉從化學悄然轉移到了另一門新興學科——熱力學與經典統計力學。
十八世紀,以蒸汽機為標志的第一次工業革命為人類社會帶來了前所未有的巨大變革。熱力學幾乎就是為了提升蒸汽機——或者更一般地說——熱機的工作效率這個現實目標而萌芽并發展起來的。對于資本家而言,一個貪婪卻無比美好的愿望是不消耗能量就能源源不斷地產生動力。但是以道爾頓的學生焦耳(J. P. Joule)為代表的物理學家通過實驗驗證了能量守恒,打破了“無中生有”的(第一類)永動機的美夢。那么退而求其次,能否讓輸入熱機的熱量全部轉化為動力,避免任何浪費呢?法國工程師卡諾(N. Carnot)提出了理想熱機的卡諾循環,明確指出無論怎樣改變工作介質或者優化機械結構,都不可能使熱機的效率達到百分之百。英國物理學家湯姆遜(W. Thomson,后來受封為開爾文勛爵,Lord Kelvin)進一步指出,不可能從單一熱源吸收熱量,并將其全部用來做功而不造成其他影響,從而宣告了“物盡其用”的(第二類)永動機的破產。德國物理學家克勞修斯(R. Clausius)在卡諾循環的基礎上提煉出熵(S)的概念,描述熱力學過程中的“能量退化”,同時給出了熱力學第二定律的數學表述:任何孤立體系的熵永不減小,并且在平衡態時達到最大值。
ΔS ≥ 0 (4)
簡明的(4)式就像一支飛箭,給熱力學的世界標注了“方向”。
雖然熱力學的誕生有著濃厚的實踐背景,但是她很快就發展為一門精巧的“唯象科學(phenomenological science)”。熱力學并不關心研究對象的微觀結構,而是用諸如內能、熵和溫度之類的狀態函數刻畫體系在接近平衡態時的宏觀性質。熱力學是如此的難以捉摸,她既能斬釘截鐵地告訴你“努力做功”的極限,又會在不經意間將你誘入“熱寂說”的哲學陷阱。于是,原子、分子學說的信奉者們非常自然地希望從物質的微觀結構出發,構建熱力學的理論基礎(mechanical theory)。他們必須解決的難題是,如何用統計的手段將大量分子的運動行為與體系的宏觀熱力學性質聯系起來,而這項努力的最終成果正是經典統計力學。

左邊:L. E. Boltzmann(1844~1906);右邊:F. W. Ostwald(1853~1932)1909年諾貝爾化學獎獲得者
在經典統計力學的發展道路上,克勞修斯最早認識到,理想氣體的內能可表達為所有氣體分子隨機運動的動能之和。英國物理學家麥克斯韋(J. C. Maxwell)則推導出了在一定溫度的平衡態下,理想氣體分子的速度分布公式,可據此計算出平衡態下處于給定速度區間的氣體分子數。一切準備工作就緒,歷史的接力棒在十九世紀七十年代交給了奧地利物理學家玻爾茲曼(L. E. Boltzmann)。經典統計力學的理論框架將在他的手中完成奠基,而這位相信并且捍衛分子理論的獨行者也將因此飽受折磨。
玻爾茲曼對于經典統計力學最重要的貢獻包括熵的統計定義,和描述理想氣體分子速度分布隨時間演化的H定理。早先,克勞修斯從熱機的工作場景出發,通過可逆過程中體系得失

亂程度”。而玻爾茲曼認為由于構成體系的大量分子的隨機運動,體系每一種確定的宏觀狀態一定對應著為數甚巨的不同微觀狀態。體系的宏觀混亂程度正是其微觀狀態多樣性的表現。因此體系某一宏觀狀態的熵S必然與對應的微觀狀態的數量W相關聯,熵值最大的平衡態所對應的微觀狀態數也必然為最大值。如果假定每種微觀狀態出現的概率相等,那么平衡態就是體系所有可能的宏觀狀態中出現概率最大的那種。為了滿足熵作為廣延量的要求(整體等于部分之和),玻爾茲曼認為體系的熵應當與其微觀狀態數的自然對數成正比。這一比例關系后來被德國物理學家普朗克(M. Planck)寫作如(5)式所示的等式(玻爾茲曼公式):

力學初學者都頗感費解,而玻爾茲曼公式為其提供了一個清晰的定義。
平衡態是熱力學最為關注的狀態。麥克斯韋的公式雖然給出了體系處于平衡態時分子運動速度的分布規律,卻無法告訴我們體系是怎樣演化到,以及為什么一定能夠演化到平衡態。玻爾茲曼用經典力學描述理想氣體分子的運動和碰撞,在假設相互碰撞的分子獨立無關(分子混沌)的條件下,得出了分子運動速度分布f隨時間演化的方程(一般稱為玻爾茲曼方程),其平衡態的解(滿足條件?f/?t = 0)正是麥克斯韋分布。玻爾茲曼進一步定義了一個關于f的泛函H(如(6)式,其中dΓ為相空間體積微元),
并證明了熱力學體系向平衡態演化的過程中H函數只減不增,且在平衡態時達到最小值(dH/dt ≤ 0),這就是著名的H定理。更為重要的是,H函數與熵呈線性負相關。H定理因此等價于斷言熱力學體系的演化過程中熵只增不減,平衡態是熵最大的狀態(dS/dt ≥ 0)。換句話說,波爾茲曼從滿足經典力學的大量分子的運動行為出發,導出了熱力學第二定律!

圖5. 位于維也納中央公墓的玻爾茲曼的墓碑,上方是熵的統計定義公式
玻爾茲曼的結論有多么令人震撼,他本人就遭受了多少非議和詰難。H定理最顯著的邏輯“漏洞”是所謂的“逆轉問題”。我們知道經典力學規律具備時間反演對稱性。如果每個分子的運動都遵循經典力學,那么由這些分子組成的集合體為什么會有確定的演化方向?如果體系從A狀態向B狀態的演化是熵增過程,那么在B狀態時令所有分子的運動速度取負值,根據時間反演對稱性,體系將反向演化到A狀態,而這個逆過程必將是熵減小的!玻爾茲曼對這一“悖論”的解釋是H定理并非力學規律,而是統計規律。宏觀體系向熵增方向的演化是大量分子運動行為的統計平均結果。雖然直到今天對H定理的內涵還沒有一個令所有人滿意的解讀,但在十九世紀末,這并不是玻爾茲曼所面臨的最致命的挑戰。相較于對數學公式理解的差異,與同時代的學者們在哲學觀點和世界觀上的爭論更給玻爾茲曼帶來了不可承受之重。
1893年起,玻爾茲曼分別在奧地利維也納大學和德國萊比錫大學任教。正是在這兩所學校,他遇到了分子理論和統計力學最強有力的反對者:萊比錫大學的奧斯特瓦爾德(F. W. Ostwald)和維也納大學的馬赫(E. Mach)。奧斯特瓦爾德雖然是一名化學家,但是他的研究與當時德國化學界的“顯學”——有機化學——頗為疏離。他從未在實驗室中發現或者合成任何一種新物質,而是特別注重運用物理學的方法,解決化學研究中的“宏大”問題。奧斯特瓦爾德被公認為“物理化學”學科的創立者,他由于在化學平衡和反應速率方面的基礎理論,以及催化領域的杰出貢獻,被授予1909年諾貝爾化學獎。奧斯特瓦爾德于1887年到萊比錫大學任教時,發表了題為“能量及其轉化”的演說,并從此致力于“能量學”的研究。熱力學在物理化學研究中所展現的巨大威力給奧斯特瓦爾德留下了深刻的印象。這使他相信,只用能量的概念就可以解釋自然界的一切現象。宇宙的根本構成要素是以各種形式存在的能量,自然規律就是支配能量流通和轉化的規律;原子、分子只是數學的虛構,物質不是能量的負荷者,而是能量的表現形式;能量學原理比分子理論更能為化學和其他科學提供堅實、明確的基礎。奧斯特瓦爾德進一步將能量學的思想上升到哲學高度,逐漸形成了“唯能論”或者“能量一元論”的世界觀。盡管奧斯特瓦爾德與玻爾茲曼保持了不錯的私交,甚至在玻爾茲曼身處困境時幫助他在萊比錫大學謀得教職。但是,1895年在德國北部港市呂貝克舉行的自然哲學家會議上,奧斯特瓦爾德公開反對分子論,和玻爾茲曼展開了激烈的辯論。分別以玻爾茲曼和奧斯特瓦爾德為首的分子論者和唯能論者互不相讓,他們的論戰貫穿了十九世紀的最后十年。
馬赫是十九世紀末極具影響力的實驗物理學家和哲學家。他在光學和流體力學的研究中取得了一系列重要的成果,如今在航空領域人們耳熟能詳的名詞“馬赫數”(表示流體速度與局部音速之比的無量綱數)就是以他的名字命名。馬赫從經驗主義的哲學觀點出發,對分子論進行了嚴厲的批判。他認為如果分子是無法被直接感知或者觀測的微小實體,那么假設它們的運動服從描述宏觀物體的經典力學規律就毫無根據。因此馬赫認為,玻爾茲曼以“分子的運動和碰撞可以用經典力學描述”為基礎得出的結論,最多不過是一種有用的數學模型,遠遠談不上分子存在的證據。面對分子論者的辯解,馬赫經常拋出的“殺手锏”就是:Have you seen one molecule(你見過分子嗎)?這時,分子論者只能悻悻而退,承認他們(暫時)還做不到這一點。畢竟從實證角度出發,反對分子論在十九世紀末與人們的經驗和邏輯并不矛盾。
玻爾茲曼的性格好強而敏感,與分子論反對者的持續爭論對他的精神狀態造成了嚴重的傷害。除了長期的抑郁情緒,晚年的玻爾茲曼還要忍受失眠、心絞痛和哮喘的折磨。1901年,玻爾茲曼離開萊比錫,回到母校維也納大學接任馬赫退休后空出的教職。雖然逃離了唯能論的大本營,但是音樂之都也沒能給擅長鋼琴的玻爾茲曼帶來足夠的撫慰。1906年9月,玻爾茲曼和家人到意大利東北部海濱城市特里雅斯特度假。在假期的最后一天,情緒失控的玻爾茲曼趁妻子和女兒去海邊游泳的空檔,在旅館的房間里上吊自殺。玻爾茲曼被安葬在維也納中央公墓,墓碑上鐫刻著以他的名字命名的熵的統計定義公式。
歷史是如此令人唏噓。假如玻爾茲曼能多活兩年,那么他將看到證實分子客觀存在的決定性實驗證據。這能否醫治好玻爾茲曼的精神創傷,我們永遠無從得知,但是奧斯特瓦爾德的確因此轉變了觀念。1909年,奧斯特瓦爾德在他撰寫的著名教科書《普通化學概論》(第三版)的序言中承認:“我們最近已經掌握了證明物質不連續本質的實驗證據”。已是風燭殘年的馬赫則仍然堅守自己的哲學觀點。1913年他出版了《物理光學原理》一書,在序言中馬赫清晰地表明:“我拒絕今天的原子論信仰。”

圖6.(左)奧斯特瓦爾德著《普通化學概論》(第三版,英譯本)序言頁面;(右)馬赫著《物理光學原理》(英譯本)序言頁面。圖中用藍線標記的是正文引用文字的出處
載入史冊的數字
十九世紀關于分子存在性的爭論從化學轉戰至熱力學與統計力學,遷延數十年而無定論,一個重要的原因是缺乏直接觀測分子的有效方法。如果能測量出某種分子的大小和質量,抑或計算出一定量的宏觀物質所包含的分子數目,局面必然為之一變。到哪里去尋找這樣的方法呢?讀者朋友們也許還記得,高中化學課在引入分子概念時,會介紹一個“用油膜法

在水面,形成一層薄薄的單分子油膜。如果測出所使用的油酸體積V(如4 × 10^(–5) cm^3)和形成的油膜面積A(如1.65 × 10^2 cm^2),就可以估測出油酸分子的線度d = V/A(約為4 × 10^(–5) cm^3 / 1.65 × 10^2 cm^2 = 2.42 × 10^(–7) cm)。
油脂在水面鋪展成膜是十分常見的現象。1773年,美國開國元勛之一富蘭克林(B. Franklin)在給友人的信中,詳細描述了他16年前的一次見聞:在海上航行的船隊中,有一兩艘船的尾部沒有明顯的航跡,船體仿佛在海面滑翔。有經驗的船長告訴富蘭克林,這一定是船上的廚師在傾倒泔水,油脂潤滑了船底的緣故。富蘭克林在倫敦南部的克拉珀姆進行了實驗。在一處被風吹皺的湖面,富蘭克林將油倒入水中,雖然油量不過一小勺,但迅速鋪展的油膜立刻讓幾平方碼的水面平靜下來。此后,他經常在竹制手杖中藏一小壺油,一有機會就向朋友們表演“平靜水面”的把戲。雖然魔術師富蘭克林時常贏得喝彩,但是考慮到他的生平年代(富蘭克林卒于1790年)和分子論發展的時間線,富蘭克林絕無可能利用油膜法估測分子的數量或者大小。
歷史上第一個估算出空氣分子大小和標準狀況(0 °C,1大氣壓)下1 cm^3空氣中所含分子數量的人是奧地利物理學家洛施密特(J. J. Loschmidt)。他也是玻爾茲曼在維也納大學求學時的老師。洛施密特計算的依據是阿伏伽德羅定律和理想氣體的分子運動論。他從克勞修斯的氣體分子平均自由程(分子在相鄰兩次碰撞之間運動的平均距離)公式出發,假定空氣分子為球體,導出其直徑s和平均自由程l滿足以下簡單關系:
s = 8εl (7)
(7)式中ε = Nπs^3/6,稱為物質的壓縮系數,它代表單位體積氣體所包含的N個球體分子自身實際占據的體積,在宏觀上近似等于物質的液態密度和標準狀況下氣態密度之比(假設液態分子小球緊密相連)。關于空氣分子的平均自由程,當時已有較多研究,洛施密特采用的數值為1.40 × 10^(–7) m。若要求得空氣分子的直徑,則必須知道空氣的壓縮系數ε。遺憾的是十九世紀六十年代人們尚未實現對空氣的液化,無法通過實驗測定液態空氣的密度。洛施密特將空氣看作由77%的氮元素和23%的氧元素組成的“化合物”,根據科柏(H. Kopp)測定的原子定容,巧妙地估計了液態空氣的密度,進而求得空氣的壓縮系數為8.66× 10^(–4)。于是可計算出空氣分子的直徑為8 × 8.66 × 10^(–4) × 1.40 × 10^(–7) m = 9.69 × 10^(–10) m(約為前文估算的油酸分子線度的三分之一,對于真實的氮氣和氧氣分子而言,該值偏大了不少)。根據這一數值,可知標準狀況下1 cm^3空氣中所含分子數量為1.83 × 10^18,這一數值有時被稱作洛施密特常數(洛施密特認為他的計算結果可能有一個數量級的誤差,該常數的現代值約為2.7 × 10^19)。洛施密特的結果在當時并沒有可靠的實驗驗證,所以影響力相對有限。想要準確計算出分子的數量,比如每“克分子”物質中所含的分子數(克分子是以克為單位、數值等于其分子量的物質質量,如氫氣的分子量為2,1克分子氫氣即2克氫氣),還需把目光聚焦于顯微鏡下,是水面上花粉微粒的無規運動,最終帶來了一枚沉甸甸的諾貝爾獎和一串載入史冊的數字。
1827年,英國植物學家布朗(R. Brown)用顯微鏡觀察懸浮在水中的花粉微粒。他發現這些微粒在不停地運動,而且軌跡雜亂無章。起初布朗認為這可能是花粉作為生命體活力的表現。但是,當他換用已經死亡的花粉微粒,或者無生命物質(如煤、巖石以及金屬)的粉末時,也能看到同樣的現象;并且運動的劇烈程度隨著微粒尺寸、液體黏度的減小,或者溫度的升高而增加。這種永不停歇的運動被命名為布朗運動。十九世紀下半葉,分子論者逐漸相信,布朗運動是由于微粒受到周圍液體分子持續不平衡的碰撞所致。正如陰極射線是湯姆遜(J. J. Thomson)發現電子的線索,布朗運動很可能成為表征分子存在的證據。只不過這項證據距離被普遍接受,還缺少一套定量理論和一組受控實驗的檢驗。
左邊:A. Einstein(1879~1955)1921年諾貝爾物理學獎獲得者;右邊:J. B. Perrin(1870~1942)1926年諾貝爾物理學獎獲得者
1905年,剛剛在蘇黎世大學獲得物理學博士學位的愛因斯坦(A. Einstein)迎來了他的“奇跡年”。他在德國《物理年鑒》期刊發表了四篇論文,極大地推進了二十世紀物理學基礎的構建。其中《熱的分子運動論所要求的靜止液體中懸浮粒子的運動》一文首次為布朗運動提供了完善的解釋。愛因斯坦認為,由于布朗粒子十分微小(線度約為10^(–4) cm),它受到來自不同方向的液體分子的撞擊不能完全抵消。在顯微鏡下觀察到的是宏觀可分辨時間內,布朗粒子受到分子頻繁撞擊所展現的平均位移,是統計規律下的漲落現象。愛因斯坦推導出了關于布朗粒子擴散的微分方程,以及粒子在給定時間內朝某一方向位移的分布公式,由此可知布朗粒子的平均位移λ與時間t的平方根成正比
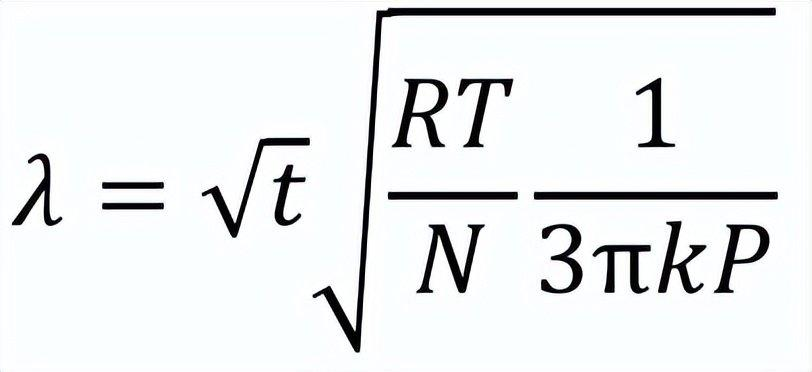
(8)
在(8)式λ和t^(1/2)的比例系數表達式中,除了普適氣體常數R,以及絕對溫度T、液體內摩擦系數k、布朗粒子的有效半徑P等可觀測量之外,就只剩下未知的每克分子物質所含的分子數N了!愛因斯坦的公式指出了一條從布朗運動的可觀測量出發,計算分子數量和大小的道路。
三年后,法國物理學家佩蘭(J. B. Perrin)走完了證實分子客觀存在的最后一步。佩蘭早年就讀于巴黎高等師范學校,后來長期在巴黎索邦大學任教。1895年佩蘭證明陰極射線中存在帶負電荷的粒子,為湯姆遜發現電子奠定了基礎。1908年,他在愛因斯坦關于布朗運動的理論啟發下,通過實驗測定了每克分子物質所含的分子數(即(8)式中的N)。為了紀念分子學說的創始人阿伏伽德羅,佩蘭建議將此數值命名為阿伏伽德羅數,記為NA。佩蘭實驗設計的關鍵在于,將檢驗布朗運動效應的方向從水平變為豎直;摒棄諸如花粉微粒之類的天然(不可控)布朗粒子體系,改用特殊制備的單分散(標準化)乳濁液作為研究對象。佩蘭認為乳濁液中的粒子由于受到重力(沉降)和布朗運動(擴散)的共同影響,在豎直方向存在數密度分布的差異(平衡態下高處的粒子數比低處少),如同大氣密度隨海拔提升而逐漸稀薄一樣。他進一步推導出了乳濁液粒子豎直方向數密度分布的公式:
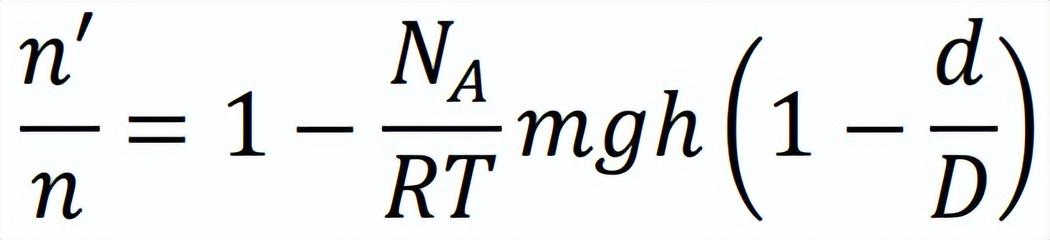
(9)
式中R和g為普適氣體常數和重力加速度。假設已知乳濁液中粒子的質量m和密度D、液體密度d以及環境溫度T,并通過實驗測定乳濁液中高度差為h的兩個水平面上的粒子數n′和n,就能計算出阿伏伽德羅數NA。
知易行難。雖然實驗原理并不復雜,但要想得到一錘定音的結果,非下一番苦功夫不可。佩蘭利用離心的方法,花費數月時間分選出幾十克粒徑高度均一的藤黃(一種繪畫顏料)和乳香(一種天然樹脂)微粒(粒徑小于0.5 μm),并準確測量了其質量和密度。他巧妙地在顯微鏡的載玻片上構建出0.1 mm高的乳濁液樣品,利用景深極淺的高倍鏡頭實現對乳濁液中單層粒子的觀測。為了克服粒子布朗運動本身對觀測的干擾,佩蘭設法將顯微鏡視場限制在針尖大小的區域,用肉眼經顯微鏡觀察某一瞬間出現在此區域中的粒子數量,經過幾千次的計數,即可求出乳濁液某一高度處的粒子數n。大道至簡,重劍無鋒。佩蘭就是利用這樣精巧又質樸的方法,對不同種類、粒徑和黏度的乳濁液在不同溫度下進行了大量重復觀測,根據(9)式計算出NA的數值為6.5~7.2 × 10^23。佩蘭和他的學生肖賽格(M. Chaudesaigues)還用顯微鏡直接觀測了乳濁液粒子布朗運動的平均位移λ,根據(8)式計算出NA的數值處于5.5~8.0 × 10^23這樣一個狹小的區間。如果扣除實驗誤差,可以認為NA對于不同物質是一個定值,阿伏伽德羅數因此可以升格為阿伏伽德羅常數。

圖7. 佩蘭在顯微鏡下拍攝的藤黃乳濁液微粒處于沉降–擴散平衡狀態時的照片。圖片來源:Advances in Colloid Science(左);Stud. Hist. Phil. Sci. 2008, 39, 312–322(右)
佩蘭對于藤黃和乳香乳濁液的觀測過程本身并不要求預先假設分子的存在,但是其觀測結果,特別是使用不同方法對NA的計算給出了高度一致的數值,就證明了愛因斯坦關于布朗運動理論的正確性,從而論證了分子的客觀存在。與唯象理論者只接受可直接感知和觀測的實驗現象不同,佩蘭指出,他的工作在肉眼可見的復雜現象與無法直接觸及的簡明原理之間建立了因果聯系(… to explain the complications of the visible in terms of invisible simplicity)。唯能論的首領奧斯特瓦爾德在佩蘭的實驗之后接受了分子的存在。法國大科學家龐加萊(H. Poincaré)——此前他和馬赫一樣認為分子只是一種無關緊要的、隨時可以放棄的數學假設——高度評價佩蘭的工作,他說:“佩蘭測定了(一定量物質所包含的)分子的數目,這一杰出的工作宣告了分子理論的勝利。”1926年,佩蘭由于對“物質不連續結構”和“發現沉降平衡”的貢獻,被授予諾貝爾物理學獎。這時距離道爾頓寫出第一張原子量表過去了123年,距離坎尼扎羅在卡爾斯魯厄會議上傳播阿伏伽德羅的分子學說過去了66年,距離玻爾茲曼自殺過去了20年。
二十世紀初,更多關于微觀世界的實驗證據和表征手段的出現,以及量子力學帶來的偉大變革,使得原子和分子的客觀存在性不再是一個爭議問題,而逐漸成為普羅大眾都有所認知的常識。1971年,第14屆國際計量大會廢止了“克分子”,重新定義“摩爾”(mole,簡寫為mol)作為物質的量的單位(摩爾也由此成為國際單位制中7個基本單位之一):規定與

原子、分子從思辨走向科學,經歷了跨越百年的追索。隨著時間的流逝,今天的人們似乎越來越把原子、分子當作理所當然的存在,而不再關心它們的歷史沿革。筆者在翻閱有關道爾頓、阿伏伽德羅、蓋–呂薩克和貝采利烏斯等人的資料時,一度對他們所關心的問題、使用的方法、發明的術語都深感隔膜、難以理解,這大概是筆者接受了20年當代化學科班訓練的結果!但是無論如何,前輩科學家們那些真正“從零到一”的探索,哪怕是他們犯的錯誤、起的爭執,都無一不值得我們細細品味。那些在黑暗中歷盡艱辛才偶有所得的、痛并快樂的歷程,可能用英國數學家懷爾斯(A. Wiles)的一段話來描述最為恰當:
“當你初入一間完全黑暗的房間,你會到處跌跌撞撞。在這個過程中,你逐漸熟悉了每一件家具的位置。終于,也許經歷了六個月的摸索,你找到了吊燈的開關。當你打開吊燈,霎時間屋里的一切被照亮,所有的陳設無不印證了你的猜想。欣喜之余,你義無反顧地打開了通往下一個黑暗房間的大門……”
參考文獻
[1] J. R. Partington, Ann. Sci. 1939, 4, 2435.
[2] A. J. Ihde, J. Chem. Educ. 1961, 38, 83.
[3] S. G. Brush, Synthese 1968, 18, 192.
[4] A. J. Rocke, Hist. Stud. Phys. Sci. 1978, 9, 225.
[5] W. W. Porterfield, J. Chem. Educ. 1995, 72, 871.
[6] M. C. Usselman, D. G. Leaist, K. D. Watson, ChemPhysChem 2008, 9, 106.
[7] M. C. Usselman, T. A. Brown, Ann. Sci. 2015, 72, 153.
[8] M. I. Grossman, Brit. J. Hist. Sci. 2017, 50, 657.
[9] Y. Xu, Y. Tong, J. Yuan, Found. Chem. 2023, 25, 439.
[10] D. S. L. Cardwell, Ed. John Dalton & The Progress of Science. Manchester University Press, 1966.
[11] A. J. Rocke, Chemical Atomism in the Nineteen Century – From Dalton to Cannizzaro. Ohio State University Press, 1984.
[12] C. Cercignani, Ludwig Boltztnann The Man Who Trusted Atoms. Oxford University Press, 1998.
[13] P. Achinstein, Book of Evidence. Oxford University Press, 2001.
[14] P. Grapí, Inspiring Air: A History of Air-related Science. Vernon Press, 2019.
[15] R. Seth, G. E. Smith, Brownian Motion and Molecular Reality. Oxford University Press, 2020.
[16] 李醒民,《自然辯證法通訊》,1988年,第10卷,57頁。
[17] 劉立,《大學化學》,1989年,第4卷,61頁。
[18] 沈乃澂,《物理》,2018年,第47卷,648頁。
[19] 王竹溪著,《熱力學》,高等教育出版社,1955年。
[20] 道爾頓著,李家玉、盛根玉譯,《化學哲學新體系》,北京大學出版社,2006年。
[21] 牛頓著,周岳明、舒幼生、邢峰、熊漢富譯,徐克明校,《牛頓光學》(第二版),北京大學出版社,2011年。
[22] 賀拉斯著,李永毅譯注,《賀拉斯詩全集——拉中對照詳注本》,中國青年出版社,2017年。
致謝
作者感謝中國科學院上海有機化學研究所游書力院士、中國科學院物理研究所曹則賢研究員、上海交通大學張紹東教授和中國科學院自然科學史研究所劉金巖研究員對本文的寶貴意見。
作者簡介
鄭超博士,中國科學院上海有機化學研究所研究員,國家自然科學基金委員會優秀青年科學基金項目獲得者。研究方向為物理有機化學與手性合成。

特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閱不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回復四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
版權說明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯系后臺。
來源: 返樸
內容資源由項目單位提供


 科普中國公眾號
科普中國公眾號
 科普中國微博
科普中國微博

 幫助
幫助
 返樸
返樸 
