我們知道CPU的主要功能就是運算，加減乘除運算的基礎是加法運算，所以我們先來看如何制作一個加法器。

我們所說的加法器當然是指二進制的加法，請看下圖：

左邊表格是二個一位二進制數相加的情況分析（二進制沒有2，只能通過進位用10描述）。目標有了，怎么實現呢？之前介紹過的異或門的邏輯與此很像（右邊的表格），我們看到前三種情況的加法，異或門可以直接實現，而最后一種情況1+1的結果是0而不是10，這里面其實缺少了一個進位，我們可以增加一個與門，解決進位的問題。

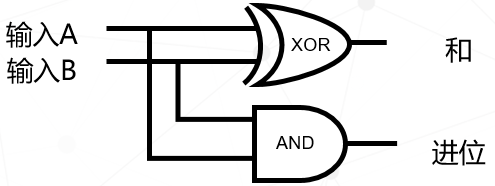
電路圖是這樣的，其中異或門的輸出作為“和的個位數”，與門的輸出作為進位。最終實現的結果如下表：

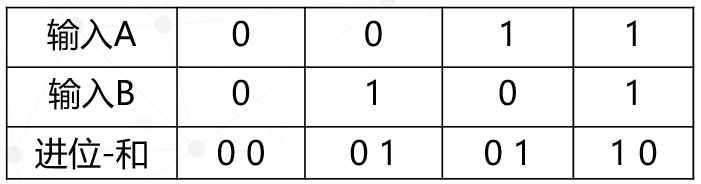
可能有人會想，1+1=10沒問題，但0+0=00,0+1=01很是奇怪，能否把前面的0去掉呢？其實我們不用擔心，這只是與我們的日常思維習慣有些沖突，并不影響結果的正確性，畢竟在一個數字前面加0和不加0的結果都一樣。

這樣我們就實現了一位二進制數的加法電路，使用這個符號表示。

為什么叫“半加器”呢？因為還不完善，因為一個完整的加法必然要考慮多位數相加，剛剛分析的只是一位數相加，如果有多位數，必然要考慮前一位數字相加后可能有進位，這個進位也要加進來，所以還可以對這個電路繼續完善，直至滿足多位數相加，這個完善的加法電路就稱為全加器，用這個符號表示。

有了半加器、全加器，就可以實現多位二進制相加了，例如二個八位二進制數相加的電路如下：

可簡化為：

減法器的過程稍顯復雜，因為減法不考慮進位，但需要考慮借位，而借的這一位如何記錄，如何歸還都是問題，所以我們要想辦法將借位化解掉。我們先從熟悉的十進制減法入手，例如35-16，用借位法很容易得出結果19，但現在我們要避免借位，怎么做呢？我們可以把式子變換一下：

35-16=35-16+100-100=35-16+99+1-100=35+（99-16）+1-100

這樣99-16就不涉及到借位，因為對于二位數來說99是最大的。我們繼續變換式子：

35+（99-16）+1-100=35+83+1-100=118+1-100=119-100

這時又遇到減法，但是不涉及借位，只需把百位的1去掉即可，結果是19。雖然看起來繞了很大一個彎路，但我們成功地避免了借位。

接下來我們來看二個八位二進制數相減的例子：

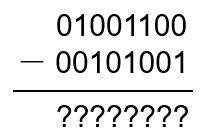
參考前面十進制減法的例子，把這個式子轉換為：

這其中涉及到二次減法，其中：

觀察一下結果會發現，差和減數是按位取反的，也就是每位0、1正好相反，這個邏輯可以使用如下電路實現：

但問題是，該電路只會對輸入取反，而我們要做的是既能做加法也能做減法的電路，所以應該在減法時實現反轉，改造電路如下：

當做減法時，取反端=1，才對輸入取反，如果是加法，取反端=0，輸入不取反。我們將這個電路簡化一下，稱為求補器：

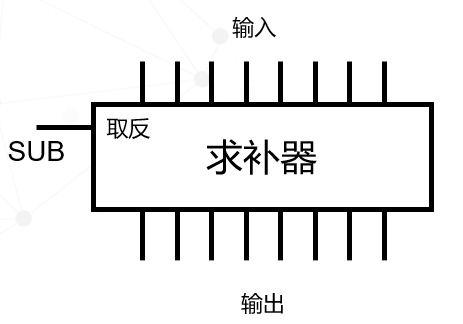
有了求補器，我們就可以將第一個減法變為加上取反后的結果：

這樣就只剩下最后一個減法，減去100000000，這個邏輯很簡單，只需將首位變為0即可，當然是在做減法的時候。終于我們將所有的減法都化解掉了，現在我們使用加法器，再配合異或門就可以實現加減法運算。

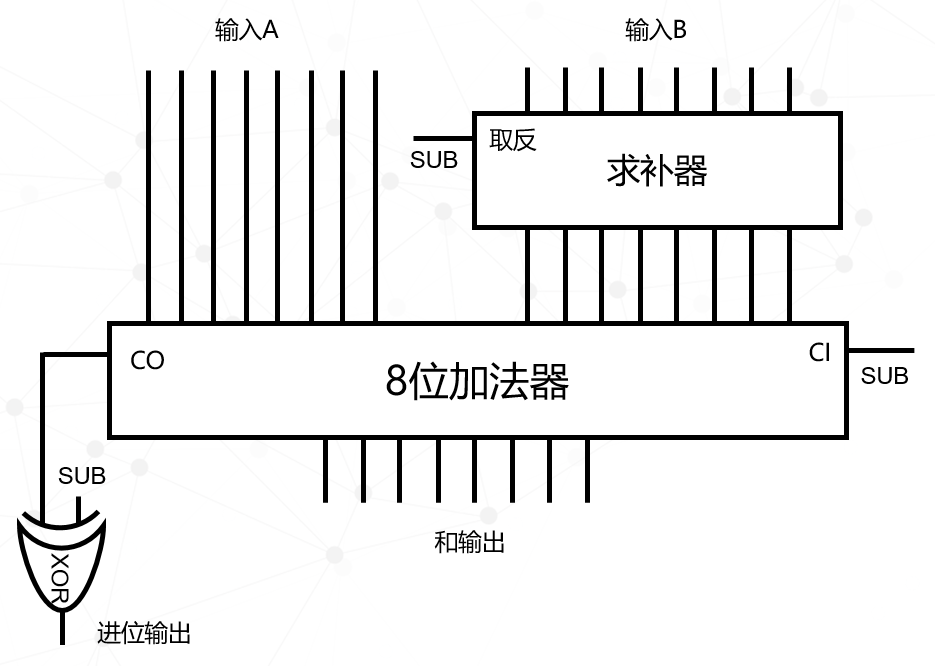
圖中有三個SUB端，這就是加減法的切換開關，當SUB=0時，進行加法運算，當SUB=1時，進行減法運算。在減法中，輸入B的數據會先通過求補器進行取反，然后再和輸入A相加。另外通過加法器的CI（進位輸入）可以實現結果+1（因為SUB=1），最后加法器的CO進位輸出（也就是結果的首位數據）通過一個異或門處理，減去1，最終得到最后的結果。

至此我們的電路已經能做加減法了，而乘法就是多次加法，除法就是多次減法，所以我們也就能實現乘除的運算了。

來源: 孫老師聊人工智能