芝諾的烏龜

芝諾是古希臘的哲學家，數學家。芝諾的烏龜（二分法悖論）是芝諾提出的四個悖論（芝諾悖論）中的第一個悖論。這四個悖論都是用來維護巴門尼德的存在學說：

存在學說：認為存在是永恒的，是太一，連續不可分；存在是不動的，是真實的，可以被思想。感性世界的具體事物是非存在，是假相，不能被思想。

換句話說，巴門尼德的存在論認為，存在是唯一真實的事物，而變化、運動、時間和空間等現象都是虛幻的。他認為，存在不可能從無到有地產生，也不可能從有到無地消失，存在是永恒、不可分割、不可變化的。因此，我們所看到的一切都是存在的不同形式和表象，而不是真正的實體。

在了解了巴門尼德的存在論，我們先來看這樣一個問題：

現在我們想要從A點走到B點，那么中途就一定會經過C點。而從C點走到B點又一定會經過D點（假設C為AB中點，D為CB中點，以此類推）那么我們就會經過無窮多個中間點，因此這個過程也會一直循環下去，這樣我們將永遠無法到達B點。

關于這個悖論，最常見解法是：

假設從A到B點需要的時間為1，那么從A到C點所需的時間就是1/2。以此類推，所以我們就可以獲得一個等比數列：

S = 1/2+1/4+1/8+1/16+...

而形如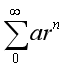的級數，如果滿足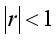，則級數收斂。因此級數S一定會收斂于一個有限值M，所以從A到B需要的時間有限。

而芝諾的烏龜描述的是，假設我們從原點開始追距離我們10米處的烏龜，那么每當我們要追到烏龜時，烏龜都會向前移動一小段距離，當我們再次前幾到烏龜移動的位置時，烏龜在我們移動的這一小段時間內又向前爬行了一段距離，以此類推。芝諾據此詭辯道，因為我們要追趕無窮多段距離，不論我們跑的有多快，永遠也無法追上爬的很慢的烏龜。

但實際上，芝諾的那個時代所不清楚的是，無窮多段距離的和可以是有限的，追趕無窮多段距離的時間之和也可以是有限的。

接下來我們來用數學推導說明一下芝諾詭辯的核心所在：

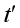這個悖論的本質是兩種不同度量的比較，一個是普通鐘，在這個普通鐘里，我們最終可以追上烏龜，而另一個就是“芝諾鐘”,在芝諾鐘里，我們將永遠無法追上烏龜。

開始時假設我們與烏龜相距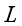，我們與烏龜的速度分別為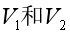，那么我們顯然有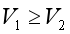。所以在普通鐘里，我們追上烏龜所需的時間為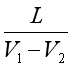。而對于芝諾鐘，假設其初始值為0，每當我們達到烏龜本來所在的位置時，其數值+1。（注意到，在假象的“芝諾時間”里，不管每次追趕距離是否越來越小，經歷的“時間”始終為1，保持不變。）比賽過程如下：

1. 比賽開始時，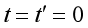

2. 我們第一次達到烏龜所在的位置，，。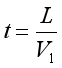

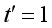3. 我們第二次達到烏龜所在的位置，，。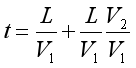

...以此類推...

4.,。

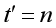因此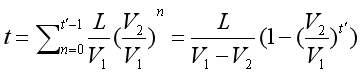

可知。畫圖可知（假設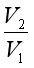為0.5）

因此當時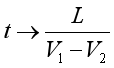，。所以從芝諾鐘的角度來看，我們永遠也無法追上烏龜。這里，芝諾把經過無窮多段距離所需要的時間都看成“1”，并沒有考慮到距離的不同所用的時間也不同，這才有了這一悖論。

關于這個問題，網絡上也有一個很有趣的回答，雖然只有一句話，但是卻能抓住這個悖論的關鍵：芝諾的烏龜這個悖論可以理解為，我們在追上烏龜之前，永遠沒辦法追上烏龜！

來源: 原創