倒立擺最初研究開始于20世紀50年代,麻省理工學院(MIT)的控制論專家根據火警發射助推器原理設計出一級倒立擺實驗設備,而后人們又參照雙足機器人控制問題研制二級倒立擺控制設備,從而提高了檢驗控制理論或方法的能力，也拓寬了控制理論或方法的檢驗范圍。三級、四級倒立擺是由一、二級倒立擺演繹而來，其實物系統控制的實現是公認的難題。

2002年8月,著名模糊理論專家李洪興教授領導的復雜系統智能控制實驗室,采用變論域自適應模糊控制在國際上首次度功實現了直線(二維)四級倒立擺的實物系統控制:2010年1月，李洪興教授領導的科研團隊又成功實現了空間四級倒工擺的實物系統控制。

通俗地講,二級倒立擺是在一個平面上運動的倒立面,n空間倒立擺則是實現了左、右、前、后以及任何方向運動的到立擺，空間四級倒立擺的實物系統控制。

（1）對安裝有fuzzy control toolbox，在示例中找到倒立擺，可以在如下畫面進行仿真。

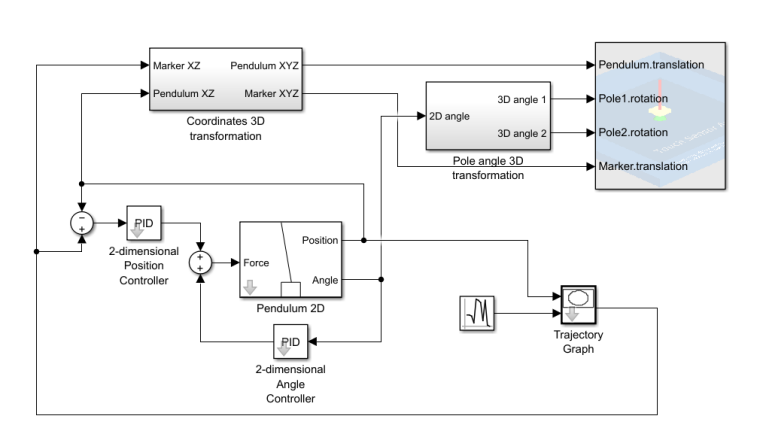
（2）雖然擺桿的偏向角0(單位:rad)保持在(一0.05,0.15)內,擺桿向左偏移沒有超過3°,向右偏移沒有超過9°,但還是不夠理想.對于精度要求要求比較高的單輸人單輸出控制系統，可采用下述方法設計模糊控制器:

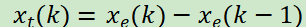
1°根據實際經驗或試驗得到輸出控制量與輸入變量偏差的一組數據,并由計算輸入變量偏差變化率,將輸入變量偏差及偏差變化率從小到大排列(表6.3).這就是說，將輸人變量偏差劃分為n個等級，輸入變量偏差變化率劃分為m個等級.

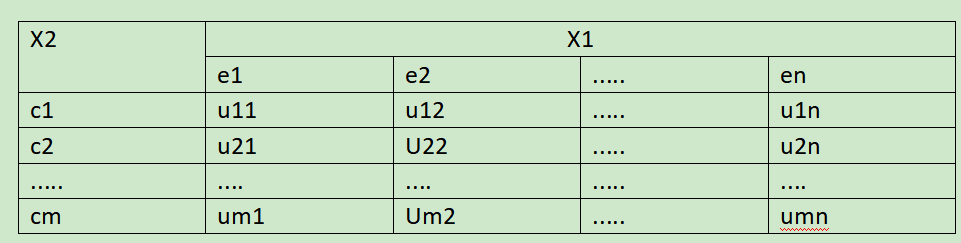
2°建立輸入變量偏差及偏差變化率各等級的隸屬函數dij(xe,xc)。隸屬函數應當滿足:當(xe,xc)∈[ej;,ej+1]X[ci,ci+1]時,除了dij,di,j+1,di+1,j,, di+1,j+1外,其他各等級的隸屬度都為零,特別當(xi,xe)=(ej,ci)時,dij=1,其他各等級的隸屬度都為零.

3°模糊判別方法:對于實際輸入變量偏差xe及偏差變化率xc，計算各等級的

隸屬度dij。，然后應用公式

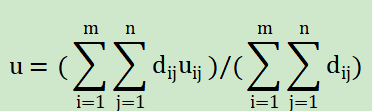
將u作為控制變量的實際輸出值.

當控制系統有特別好的線性性時,更直接地采用簡化公式，如下面例子所示。

例倒擺的模糊控制器的設計(二)

由于倒擺的控制系統有特別好的線性性,可直接采用下列公式

u=20.75xe+0.25xc。

倒擺的 MATLAB計算機仿真程序如下:

A=[1,1,0,0;20.601,1,0,0;0,0,1,1;-0.4905,0,0,1];

B=[0,-1,0,0.5]';%仿真矩陣

x(1,1)=0.3;x(2,1)=0;x(3,1)=0;x(4,1)=0;%賦初值

for(k=1:200) %進行 200次仿真實驗

xe=x(1,k);xc=0;%計算輸入變量偏差

if(k>1)xc=x(1,k)-x(1,k-1);

end %計算輸入變量偏差的變化率

u(k)=20.75*xe+0.25*xc;%計算實際輸出量

x(:,k+1)=A*x(:,k)+B*u(k); %由倒擺運動方程進行仿真

end

t=1:201; y=x(1,:); plot(t,y); %

來源: 成信大，部分來自書籍