微積分?聽起來很高大上!我也能懂嗎?
作者鄭重承諾:讀懂這篇科普最多需要初中數學知識!而且大部分不需要數學知識,只需要觀察力和想象力!
微積分是高等數學的重要組成部分。它表現了運動和變化的思想,讓數學從靜態走向動態。上至三體問題,下至投籃拋物,要想精確求解,都離不開微積分這一工具。
微積分主要包含三大部分:極限論、微分學、積分學(這會兒知道為什么叫“微積分”了吧?)。
這次微積分科普,會圍繞我們的老朋友進行:圓周率π。
沒錯!就是圓的周長與直徑的比,是一個無限不循環小數:3.1415926……
今年是中國古代數學家劉徽誕辰1800周年。劉徽為了得出準確的圓周率,創造了一種名叫“割圓術”的算法。所謂“割圓”,就是畫圓內接正多邊形,增加邊數。他說:“割之彌細,所失彌少。割之又割,以至于不可割,則與圓周合體而無所失矣。”
這里有一個重要概念:無限。一個重要方法:逼近。
看這張圖,隨著邊數增加,多邊形越來越接近圓,其周長也越來越接近圓的周長。
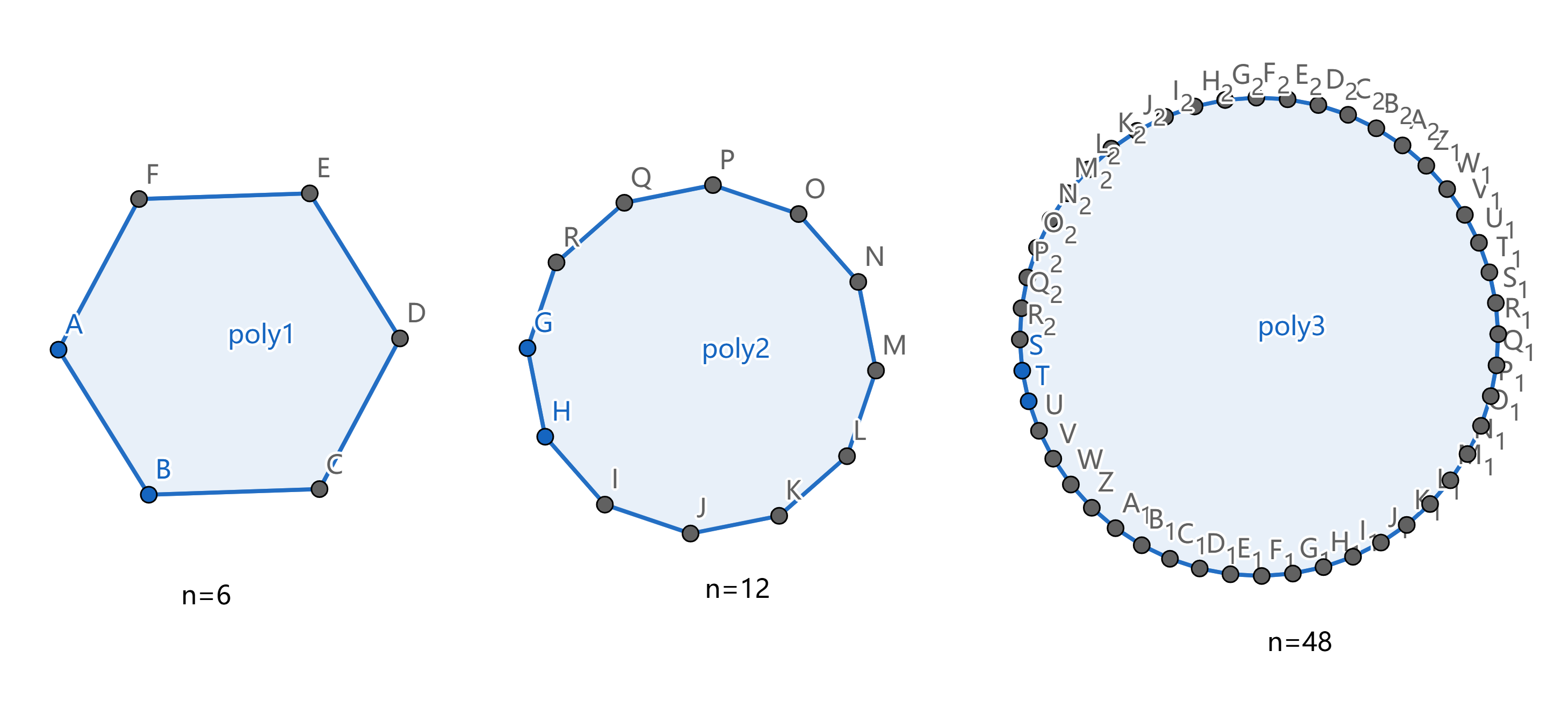
為了思考無限,我們用越來越大的數字來逼近它。48條邊的正多邊形,雖然不是“無限”條邊,但也很接近圓了吧?所以我們稍微想象一下,就可以猜到:有無限條邊時,多邊形就變成了圓!
上面的過程體現了“極限思想”。所謂極限,就是“趨勢”。我們把直徑為1的正六邊形的周長記做C6,正12邊形周長是C12……以此類推。
看這一串數:C6=3,C12≈3.096……Cn。當n越來越大的時候,Cn就越來越接近π。
換句話說,當n大到一定程度的時候(比如n=48),Cn與π的“距離”非常小。數學上用兩個數的差的絕對值,來描述它們的距離。
再精細一些,把上面的“一定程度”換成某個大數N,“非常小的距離”換成任意的正數。當邊數n大于N時,Cn-π的絕對值(距離)小于一個任意小的正數ε(N越大ε越小)。這時把π稱為數列Cn的極限,稱“Cn趨于π”。
這就是數列極限的定義。
讓我們回到用割圓術求π,思路是這樣的:
求π只需求出圓的周長,再除以直徑。首先是把正n邊形的邊長累加,然后,讓n一直增大。當n趨于無窮大,累計周長就趨于π了。
所以我們不急于讓n變大。先固定n,得出累加表達式,再求極限!
看這張圖(以n=6為例),我們把圓畫在一個坐標系里,圓心就是原點。把正n邊形邊長寫作ds(前面加d表示“非常小”),邊長的水平距離是dx,垂直距離是dy。

現在要用到初中的“勾股定理”:
ds2=dx2+dy2.
但同時知道dx、dy有點麻煩,可以換一種寫法,只保留dx嗎?
我們現在處理的是直線,初中數學有“斜率”k的概念。在這里,k=dy/dx。所以dy=k?dx.
換一種寫法:
ds2=dx2+k2dx2=(1+k2)dx2.
那么,正n邊形的周長就是:
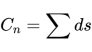
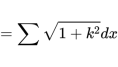
等號右邊的怪符號表示求和。
因為在多邊形不同的邊上,k是不一樣的。當n越來越大時,ds越來越短,dx也越來越短,多邊形上每一點就對應一個斜率k。當我們用dx代替n來表示周長Cn,這個式子就是以多邊形上一點的橫坐標x為自變量的函數。
函數極限的定義與數列極限類似:當Cn與π的距離小于任意正數ε(非常近),如果有正數δ,dx與0的距離小于δ。這時就叫dx趨于0時,Cn趨于π。
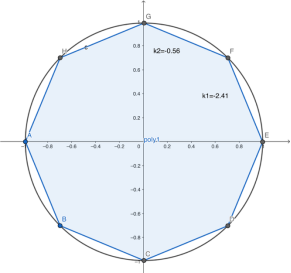
當n趨于無窮大(dx趨于0)時,正多邊形不復存在,k的幾何意義是什么呢?
我們以任意一條邊為例觀察:邊與圓有兩個交點,這種線叫做圓的“割線”。我們固定其中一點,當n增大,割線與圓的兩個交點越來越近,最終會是什么呢?
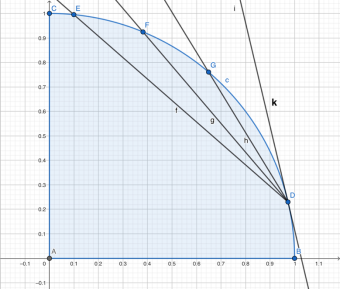
兩個交點合而為一!割線變成了切線!
所以,當n趨于無窮大,k的幾何意義就是該點切線的斜率!
在微積分中,我們把k叫做“導數”,如圖所示的k就是函數y=f(x)在點D處的導數。
導數可表示為
f(x)'=dy/dx.
導數是微分學的核心。
如果把上式換個寫法:
dy=f(x)'dx.
又是什么意思呢?
dx是一段非常小的橫向距離(x的變化量),乘上x的導數之后,就是對應的縱向距離。如果知道了函數f(x),而且點(x,f(x))存在導數,就可以根據求導法則求出f(x)在該點的導數,借此得到dy。當dx非常小的時候,dy非常接近于y的變化量。也就是說,可以用直線估計曲線!在微積分角度看,只有把dx取得足夠小,曲線的微觀部分就是直線!
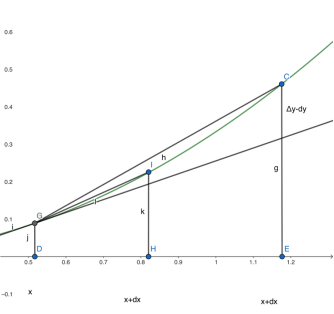
由圖片可知,當dx越來越接近0,y的變化量Δy和dy的差就越來越小,最終可以用dy估計Δy的變化量(曲線也越來越接近直線)。
這時,我們把dy叫做“微分”。
需要指出,導數和微分存在的前提是函數連續。借助圖像來說,如果圓有缺口,缺口處就沒有切線!因此該點沒有導數和微分!
反過來,如函數可導,則函數連續。
現在回到求圓周率,我們要算的是n趨于無窮大時累計和的極限。
把累計和表示為:
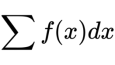
其中x的大小在兩個實數a、b之間。
如果函數f(x)是連續的,那么dx趨于0時,累計和的極限叫做“定積分”。a叫積分下限,b叫積分上限。寫作:
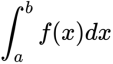
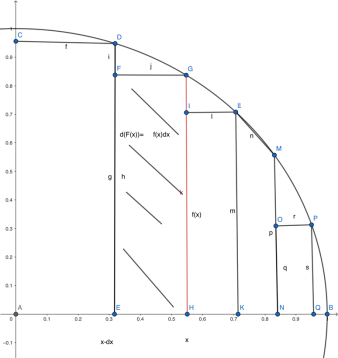
我們知道dx是橫向的一小段,而對每一個dx,f(x)是對應的函數值,所以f(x)dx就是一個窄矩形的面積(如圖)。對這一系列矩形求和,取極限(dx趨于0),就是函數f(x)下曲邊梯形的面積(由函數圖像、x軸、縱向直線x=a和x=b圍成)!這就是積分的幾何意義。
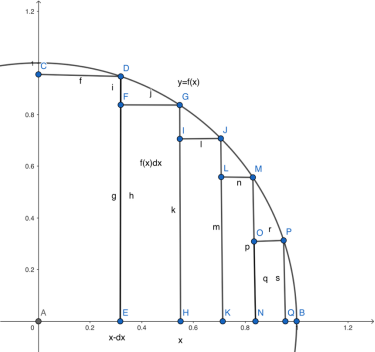
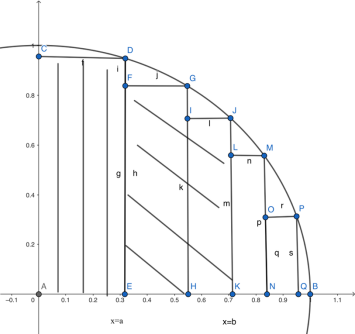
斜線陰影部分即x=a、x=b之間的曲邊梯形
但是我們剛才只掌握了微分學,如何把求面積跟微分學建立聯系呢?微分是“化整為零”從而“化曲為直”,而積分是“化整為零”之后“集腋成裘”,二者好像很難關聯起來。
數學有一個重要思維叫“化歸”,也就是重新表達問題,使之變成已經解決的問題。我們現在需要造出一座橋梁,把積分和微分打通!
接下來介紹一個重磅公式:牛頓-萊布尼茨公式。
我們提出一個新函數,叫“原函數”:
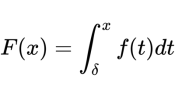
其中,t是自變量(δ≤t≤ε),函數f(t)在這一區域存在積分,x也在這一區域中。
根據定積分的幾何意義,原函數就是f(t)、水平軸、直線t=δ和t=x圍成的曲邊梯形的面積。
由上圖可得,我們要求的面積,是自δ到b的面積減去δ到a的面積(陰影部分減豎線陰影部分,就是斜線陰影部分),所以用數學語言表達:
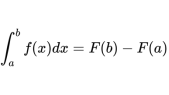
那么,只要把原函數F(x)和微分學建立聯系,問題就解決了!
現在思考一個問題:對F(x)求導數(自變量為x),會得到什么?
我們已經知道,函數f(x)的導數可表示為dy/dx。dx趨于0時,dy是函數變化量。
根據定積分的幾何性質,可以知道原函數的變化量是一個很窄的曲邊梯形,面積就是f(x)dx。現在把它再“除”dx,得到的就是f(x)!所以,對一個函數求原函數后,再求導數,會得到最初的函數!換句話說,求原函數是求導的逆運算(就像加法是減法的逆運算)。積分和微分成功建立了聯系!
因此,F(x)’=f(x)。
如果幾個函數只相差一個任意常數,對它們求導的結果是一樣的(平移曲線不會改變形狀,所以各點斜率不變)。用C表示常數,則
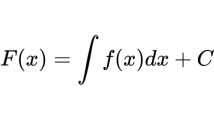
我們把新式子中的
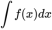
稱為不定積分。根據求原函數與求導之間是逆運算的關系,給出不定積分表。可以通過不定積分表,借助牛頓-萊布尼茨公式求解面積!概括說就是:求面積就是求定積分,求定積分就需要求原函數,求原函數就查不定積分表!
為了方便,也把求原函數叫做“求積分”。
說了這么多,π怎么算啊?接下來就是收尾大戲:
為了便于計算,令圓半徑為1。此時周長為2π,半周長的大小就是π。因為圓是對稱的,只需算出圓周長的四分之一,再乘以2就是半周長,也就是π。
因為x的取值范圍是0到1(半徑為一),因此圓四分之一周長就是
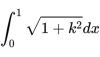
剛才我們說了,k就是圓在某點的導數。因為圓的方程是
y2+x2=1
四分之一的圓的方程(x、y都大于0)就是
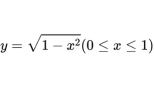
根據求導公式,得出導數

代入k得
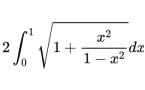
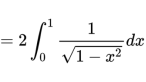
=2(F(1)-F(0))
根據不定積分表,

arcsin(x)是正弦函數的反函數,就是把正弦函數的x和y顛倒過來,比如sin(π/2)=1,則arcsin(1)=π/2(π/2就是90度)。
因此,
2(F(1)-F(0))
=2arcsin(1)-2arcsin(0)
=2(π/2)
=π
因此,我們用微積分方法,也能算出圓周率!
我們從割圓術出發,討論了微積分的幾個重要部分:極限、微分學、積分學。最后用微積分重新算出了圓周率。
下面回顧一下:
割圓術的實質,是用短小的直邊逼近圓周的曲線。當我們把圓周無限細分,可以把幾乎看不出彎曲的短曲線看成直線。然后把這些直線的長度求和,就相當于圓的周長。
這里面有兩個過程。第一個是切割:在圓內作越來越短的割線,割線最后會成為與圓只有一個交點的切線,把這段非常短小的切線長代替局部的曲線長。切線的斜率叫“導數”。
第二個過程是把這些細微的短線求和,積少成多,求割線趨于0時的極限,稱為“積分”。
不論微分還是積分,都必須有一個前提:曲線必須是完整的,不可以有缺口——因為直線與缺口沒有交點,就沒有切線。換句話說,曲線必須連續!因此,連續是微分、積分的前提。把有限的長度切分成一系列細微部分,用越切越細的過程逼近結果,是微分、積分的基礎。
參考文獻:
[1]常庚哲,史濟懷編.數學分析教程.上冊[M].北京:高等教育出版社,2003.5
[2][日]小平邦彥著;裴東河譯.微積分入門[M].北京:人民郵電出版社,2019.3
來源: 陳林孝


 科普中國公眾號
科普中國公眾號
 科普中國微博
科普中國微博

 幫助
幫助
 陳林孝
陳林孝 
