經濟博弈論之斯塔克博格模型

引言

2012年河谷公司、力拓公司、必和必拓公司對未來鐵礦的預期不同。河谷和力拓選擇擴大鐵礦石而必和必拓則比較保守。三年之后即2015年必和必拓也在增加產量。

由此可知，2012年必和必拓就預計會出產能過剩的情況但是之后卻仍然選擇增加產能。

圖源百度

為什么會出現這樣的情況呢？

必和必拓的做法正確嗎？

接下來就讓我們進入今天的學習科普來分析這種動態的寡頭市場產量博弈模型——斯塔克博格模型（Stackelberg Competition）。

假設

有兩個寡頭，廠商1和廠商2。廠商1先選擇自己的產量，廠商2根據廠商1的選擇之后再選擇自己的產量。

Q=q1+q2 產量

p=p(Q)=a-(q1+q2) 價格是與產量之間的函數

MC=c 邊際生產成本

接下來需要寫出博弈的一些內容

參與者：N={1,2}

策略式：Si={qi|qi∈（0，∞）}

收益即利潤函數：πi=（p-c）qi

之后計算兩個廠商之間的收益為

π1=q1p(Q)-cq1=q1(a-q1-q2)-cq1=(a-c)q1-q12-q1q2

π2=q2p(Q)-cq2=q2(a-q1-q2)-cq2=(a-c)q2-q22-q1q2

根據逆向歸納法，先分析第二階段廠商2的決策，在廠商2決策時，廠商1選擇的q1已經是確定了的了。因此可以展示為在給定q1的情況下是π2最大化的q2*。因此q2*必須滿足如下條件：

（a-c）-q1-2q2*=0

即q2*=（a-c-q1）/2

廠商1知道廠商2的思路之后，在選擇產量q1時會按照q2*所決定。所以決定q1*時，是將q2*直接代入

π1=(a-c)q1-q12-q1[（a-c-q1）/2]=(a-c)q1/2-q12/2

之后對q1求偏導可得

（a-c）/2-q1*=0

即q1*=（a-c）/2

同理在廠商2知道廠商1選擇q1*時，它的收益會是

π2=(a-c)q2-q22-[(a-c)/2]q2=（a-c）/2-q2-q22

求偏導可得

（a-c）/2-2q2*=0

q2*=（a-c）/4

因此q1=（a-c）/2 q2=（a-c）/4就是這個動態博弈中的子博弈完美納什均衡。

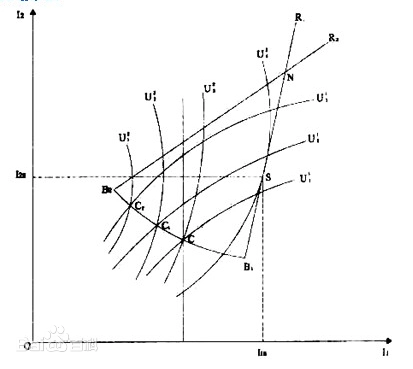
圖源百度

斯塔克伯格模型均衡的總產量多，價格較低，總收益也較少，這就說明在信息不對稱的博弈中，信息較多的參與者（廠商2）最終不一定會得到較多的收益。在引言中的必和必拓公司也是如此，它的決策可能是正確的，但也不會有很高的收益。

來源: 北京理工大學